
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏy=-![]() x2+bx+c”κΉχ±ξ÷αΖ÷±πΫΜ”ΎΒψAΘ®0Θ§8Θ©ΓΔBΘ®8Θ§0Θ©ΚΆΒψEΘ§Ε·ΒψC¥”‘≠ΒψOΩΣ Φ―ΊOAΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»“ΤΕ·Θ§Ε·ΒψD¥”ΒψBΩΣ Φ―ΊBOΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»“ΤΕ·Θ§Ε·ΒψCΓΔDΆ§ ±≥ωΖΔΘ§Β±Ε·ΒψDΒΫ¥ο‘≠ΒψO ±Θ§ΒψCΓΔDΆΘ÷Ι‘ΥΕ·Θ°
x2+bx+c”κΉχ±ξ÷αΖ÷±πΫΜ”ΎΒψAΘ®0Θ§8Θ©ΓΔBΘ®8Θ§0Θ©ΚΆΒψEΘ§Ε·ΒψC¥”‘≠ΒψOΩΣ Φ―ΊOAΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»“ΤΕ·Θ§Ε·ΒψD¥”ΒψBΩΣ Φ―ΊBOΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»“ΤΕ·Θ§Ε·ΒψCΓΔDΆ§ ±≥ωΖΔΘ§Β±Ε·ΒψDΒΫ¥ο‘≠ΒψO ±Θ§ΒψCΓΔDΆΘ÷Ι‘ΥΕ·Θ°
Θ®1Θ©÷±Ϋ”–¥≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΚ ΘΜ
Θ®2Θ©«σΓςCEDΒΡΟφΜΐS”κDΒψ‘ΥΕ· ±ΦδtΒΡΚ· ΐΫβΈω ΫΘΜΒ±tΈΣΚΈ÷Β ±Θ§ΓςCEDΒΡΟφΜΐΉν¥σΘΩΉν¥σΟφΜΐ «Εύ…ΌΘΩ
Θ®3Θ©Β±ΓςCEDΒΡΟφΜΐΉν¥σ ±Θ§‘Ύ≈ΉΈοœΏ…œ «Ζώ¥φ‘ΎΒψPΘ®ΒψE≥ΐΆβΘ©Θ§ ΙΓςPCDΒΡΟφΜΐΒ»”ΎΓςCEDΒΡΉν¥σΟφΜΐΘΩ»τ¥φ‘ΎΘ§«σ≥ωPΒψΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©y=-![]() x2+3x+8
x2+3x+8
Θ®2Θ©
ΫβΘΚΓΏΒψAΘ®0Θ§8Θ©ΓΔBΘ®8Θ§0Θ©Θ§
ΓύOA=8Θ§OB=8Θ§
Ννy=0Θ§ΒΟΘΚ-![]() x2+3x+8=0Θ§
x2+3x+8=0Θ§
ΫβΒΟΘΚx18Θ§x2=2Θ§
ΓΏΒψE‘Ύx÷αΒΡΗΚΑκ÷α…œΘ§
ΓύΒψEΘ®-2Θ§0Θ©Θ§
ΓύOE=2Θ§
ΗυΨίΧβ“βΒΟΘΚΒ±DΒψ‘ΥΕ·tΟκ ±Θ§BD=tΘ§OC=tΘ§
ΓύOD=8©¹tΘ§
ΓύDE=OE+OD=10©¹tΘ§
ΓύS=![]() DEOC=
DEOC=![]() Θ®10-tΘ©t=-
Ȯ10-tȩt=-![]() t2+5tȧ
t2+5tȧ
Φ¥S=-![]() t2+5t=-
t2+5t=-![]() Θ®t-5Θ©2+
Θ®t-5Θ©2+![]() Θ§
Θ§
ΓύΒ±t=5 ±Θ§SΉν¥σ=![]()
Θ®3Θ©
”…Θ®2Θ©÷ΣΘΚΒ±t=5 ±Θ§SΉν¥σ=![]() Θ§
Θ§
ΓύΒ±t=5 ±Θ§OC=5Θ§OD=3Θ§
ΓύCΘ®0Θ§5Θ©Θ§DΘ®3Θ§0Θ©Θ§
”…Ι¥Ι…Ε®άμΒΟΘΚCD=![]() Θ§
Θ§
…η÷±œΏCDΒΡΫβΈω ΫΈΣΘΚy=kx+bΘ§
ΫΪCΘ®0Θ§5Θ©Θ§DΘ®3Θ§0Θ©Θ§¥ζ»κ…œ ΫΒΟΘΚ
k=-![]() Θ§b=5Θ§
Θ§b=5Θ§
Γύ÷±œΏCDΒΡΫβΈω ΫΈΣΘΚy=-![]() x+5Θ§
x+5Θ§
ΙΐEΒψΉςEFΓΈCDΘ§ΫΜ≈ΉΈοœΏ”κΒψPΘ§»γΆΦ1Θ§
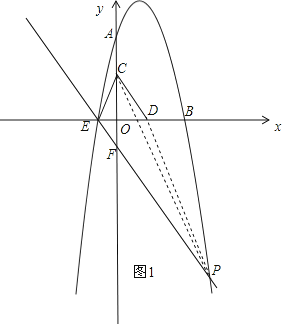
…η÷±œΏEFΒΡΫβΈω ΫΈΣΘΚy=-![]() x+bΘ§
x+bȧ
ΫΪEΘ®-2Θ§0Θ©¥ζ»κΒΟΘΚb=-![]() Θ§
Θ§
Γύ÷±œΏEFΒΡΫβΈω ΫΈΣΘΚy=-![]() x-
x-![]() Θ§
Θ§
ΫΪy=-![]() x-
x-![]() Θ§”κy=-
Θ§”κy=-![]() x2+3x+8ΝΣΝΔ≥…ΖΫ≥ΧΉιΒΟΘΚ
x2+3x+8ΝΣΝΔ≥…ΖΫ≥ΧΉιΒΟΘΚ
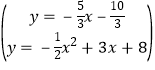 Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§ Θ§
Θ§
ΓύPΘ®![]() Θ§©¹
Θ§©¹![]() Θ©ΘΜ
Θ©ΘΜ
ΙΐΒψEΉςEGΓΆCDΘ§¥ΙΉψΈΣGΘ§
ΓΏΒ±t=5 ±Θ§SΓςECD=![]() =
=![]() Θ§
Θ§
ΓύEG=![]() Θ§
Θ§
ΙΐΒψDΉςDNΓΆCDΘ§¥ΙΉψΈΣNΘ§«“ ΙDN=![]() Θ§ΙΐΒψNΉςNMΓΆx÷αΘ§¥ΙΉψΈΣMΘ§»γΆΦ2Θ§
Θ§ΙΐΒψNΉςNMΓΆx÷αΘ§¥ΙΉψΈΣMΘ§»γΆΦ2Θ§
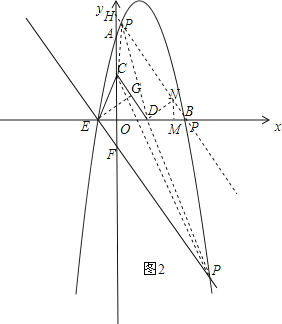
Ω…ΒΟΓςEGDΓΉΓςDMNΘ§
Γύ![]() Θ§
Θ§
Φ¥ΘΚ![]() Θ§
Θ§
ΫβΒΟΘΚDM=![]() Θ§
Θ§
ΓύOM=![]() Θ§
Θ§
”…Ι¥Ι…Ε®άμΒΟΘΚMN=![]() =
=![]() Θ§
Θ§
ΓύNΘ®![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
ΙΐΒψNΉςNHΓΈCDΘ§”κ≈ΉΈοœΏΫΜ”κΒψPΘ§»γΆΦ2Θ§
…η÷±œΏNHΒΡΫβΈω ΫΈΣΘΚy=-![]() x+bΘ§
x+bȧ
ΫΪNΘ®![]() Θ§
Θ§![]() Θ©Θ§¥ζ»κ…œ ΫΒΟΘΚb=
Θ©Θ§¥ζ»κ…œ ΫΒΟΘΚb=![]() Θ§
Θ§
Γύ÷±œΏNHΒΡΫβΈω ΫΈΣΘΚy=-![]() x+
x+![]() Θ§
Θ§
ΫΪy=-![]() x+
x+![]() Θ§”κy=-
Θ§”κy=-![]() x2+3x+8ΝΣΝΔ≥…ΖΫ≥ΧΉιΒΟΘΚ
x2+3x+8ΝΣΝΔ≥…ΖΫ≥ΧΉιΒΟΘΚ
 Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§ Θ§
Θ§
ΓύPΘ®8Θ§0Θ©ΜρPΘ®![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
Ήέ…œΥυ ωΘΚΒ±ΓςCEDΒΡΟφΜΐΉν¥σ ±Θ§‘Ύ≈ΉΈοœΏ…œ¥φ‘ΎΒψPΘ®ΒψE≥ΐΆβΘ©Θ§ ΙΓςPCDΒΡΟφΜΐΒ»”ΎΓςCEDΒΡΉν¥σΟφΜΐΘ§ΒψPΒΡΉχ±ξΈΣΘΚPΘ®![]() Θ§-
Θ§-![]() Θ©ΜρPΘ®8Θ§0Θ©ΜρPΘ®
Θ©ΜρPΘ®8Θ§0Θ©ΜρPΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩΘ®1Θ©ΫΪΒψAΘ®0Θ§8Θ©ΓΔBΘ®8Θ§0Θ©¥ζ»κ≈ΉΈοœΏy=©¹![]() x2+bx+cΦ¥Ω…«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=©¹
x2+bx+cΦ¥Ω…«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=©¹![]() x2+3x+8ΘΜ
x2+3x+8ΘΜ
Θ®2Θ©ΗυΨίΧβ“βΒΟΘΚΒ±DΒψ‘ΥΕ·tΟκ ±Θ§BD=tΘ§OC=tΘ§»ΜΚσ”…ΒψAΘ®0Θ§8Θ©ΓΔBΘ®8Θ§0Θ©Θ§Ω…ΒΟOA=8Θ§OB=8Θ§¥”ΕχΩ…ΒΟOD=8©¹tΘ§»ΜΚσΝνy=0Θ§«σ≥ωΒψEΒΡΉχ±ξΈΣΘ®©¹2Θ§0Θ©Θ§ΫχΕχΩ…ΒΟOE=2Θ§DE=2+8©¹t=10©¹tΘ§»ΜΚσάϊ”Ο»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΦ¥Ω…«σΓςCEDΒΡΟφΜΐS”κDΒψ‘ΥΕ· ±ΦδtΒΡΚ· ΐΫβΈω ΫΈΣΘΚS=©¹![]() t2+5tΘ§»ΜΚσΉΣΜ·ΈΣΕΞΒψ ΫΦ¥Ω…«σ≥ωΉν÷ΒΈΣΘΚSΉν¥σ=
t2+5tΘ§»ΜΚσΉΣΜ·ΈΣΕΞΒψ ΫΦ¥Ω…«σ≥ωΉν÷ΒΈΣΘΚSΉν¥σ=![]() ΘΜ
ΘΜ
Θ®3Θ©”…Θ®2Θ©÷ΣΘΚΒ±t=5 ±Θ§SΉν¥σ=![]() Θ§ΫχΕχΩ…÷ΣΘΚΒ±t=5 ±Θ§OC=5Θ§OD=3Θ§ΫχΕχΩ…ΒΟCD=
Θ§ΫχΕχΩ…÷ΣΘΚΒ±t=5 ±Θ§OC=5Θ§OD=3Θ§ΫχΕχΩ…ΒΟCD=![]() Θ§¥”Εχ»ΖΕ®CΘ®0Θ§5Θ©Θ§DΘ®3Θ§0Θ©»ΜΚσΗυΨί¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏCDΒΡΫβΈω ΫΈΣΘΚy=©¹
Θ§¥”Εχ»ΖΕ®CΘ®0Θ§5Θ©Θ§DΘ®3Θ§0Θ©»ΜΚσΗυΨί¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏCDΒΡΫβΈω ΫΈΣΘΚy=©¹![]() x+5Θ§»ΜΚσΙΐEΒψΉςEFΓΈCDΘ§ΫΜ≈ΉΈοœΏ”κΒψPΘ§»ΜΚσ«σ≥ω÷±œΏEFΒΡΫβΈω ΫΘ§”κ≈ΉΈοœΏΝΣΝΔΖΫ≥ΧΉιΫβΒΟΦ¥Ω…ΒΟΒΫΤδ÷–ΒΡ“ΜΗωΒψPΒΡΉχ±ξΘ§»ΜΚσάϊ”ΟΟφΜΐΖ®«σ≥ωΒψEΒΫCDΒΡΨύάκΈΣΘΚ
x+5Θ§»ΜΚσΙΐEΒψΉςEFΓΈCDΘ§ΫΜ≈ΉΈοœΏ”κΒψPΘ§»ΜΚσ«σ≥ω÷±œΏEFΒΡΫβΈω ΫΘ§”κ≈ΉΈοœΏΝΣΝΔΖΫ≥ΧΉιΫβΒΟΦ¥Ω…ΒΟΒΫΤδ÷–ΒΡ“ΜΗωΒψPΒΡΉχ±ξΘ§»ΜΚσάϊ”ΟΟφΜΐΖ®«σ≥ωΒψEΒΫCDΒΡΨύάκΈΣΘΚ![]() Θ§»ΜΚσΙΐΒψDΉςDNΓΆCDΘ§¥ΙΉψΈΣNΘ§«“ ΙDN=
Θ§»ΜΚσΙΐΒψDΉςDNΓΆCDΘ§¥ΙΉψΈΣNΘ§«“ ΙDN=![]() Θ§»ΜΚσ«σ≥ωNΒΡΉχ±ξΘ§»ΜΚσΙΐΒψNΉςNHΓΈCDΘ§”κ≈ΉΈοœΏΫΜ”κΒψPΘ§»ΜΚσ«σ≥ω÷±œΏNHΒΡΫβΈω ΫΘ§”κ≈ΉΈοœΏΝΣΝΔΖΫ≥ΧΉι«σΫβΦ¥Ω…ΒΟΒΫΤδ÷–ΒΡΝμΝΫΗωΒψPΒΡΉχ±ξΘ°
Θ§»ΜΚσ«σ≥ωNΒΡΉχ±ξΘ§»ΜΚσΙΐΒψNΉςNHΓΈCDΘ§”κ≈ΉΈοœΏΫΜ”κΒψPΘ§»ΜΚσ«σ≥ω÷±œΏNHΒΡΫβΈω ΫΘ§”κ≈ΉΈοœΏΝΣΝΔΖΫ≥ΧΉι«σΫβΦ¥Ω…ΒΟΒΫΤδ÷–ΒΡΝμΝΫΗωΒψPΒΡΉχ±ξΘ°


 –ΡΥψΩΎΥψ«…Υψ“ΜΩΈ“ΜΝΖœΒΝ–¥πΑΗ
–ΡΥψΩΎΥψ«…Υψ“ΜΩΈ“ΜΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫ––ΥΡ±Ώ–ΈABCD÷–Θ§AB=6Θ§AD=9Θ§ΓœBADΒΡΤΫΖ÷œΏΫΜBC”ΎΒψEΘ§ΫΜDCΒΡ―”≥ΛœΏ”ΎΒψFΘ§BGΓΆAEΘ§¥ΙΉψΈΣGΘ§BG=4 ![]() Θ§‘ρΓςCEFΒΡ÷ή≥ΛΈΣ Θ°
Θ§‘ρΓςCEFΒΡ÷ή≥ΛΈΣ Θ° 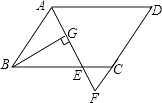
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ
Θ®1Θ©ΦΤΥψΘΚ©¹Θ®©¹2Θ©+Θ®1+Π–Θ©0©¹|![]() |+
|+![]() ΘΜ
ΘΜ
Θ®2Θ©œ»Μ·ΦρΘ§‘Ό«σ÷ΒΘΚΘ®x+2Θ©Θ®x©¹2Θ©©¹xΘ®x+3Θ©Θ§Τδ÷–x=©¹3Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“‘ABCOΒΡΕΞΒψOΈΣ‘≠ΒψΘ§±ΏOCΥυ‘Ύ÷±œΏΈΣx÷αΘ§Ϋ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§ΕΞΒψAΓΔCΒΡΉχ±ξΖ÷±π «Θ®2Θ§4Θ©ΓΔΘ®3Θ§0Θ©Θ§ΙΐΒψAΒΡΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσΫΜBC”ΎDΘ§Ν§Ϋ”ADΘ§‘ρΥΡ±Ώ–ΈAOCDΒΡΟφΜΐ « Θ°
ΒΡΆΦœσΫΜBC”ΎDΘ§Ν§Ϋ”ADΘ§‘ρΥΡ±Ώ–ΈAOCDΒΡΟφΜΐ « Θ° 
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫ–ΈABCDΒΡΆβ≤ύΘ§ΉςΒ»±Ώ»ΐΫ«–ΈCDEΘ§Ν§Ϋ”AEΘ§BEΘ§‘ρΓœAEBΒΡΕ» ΐΈΣ Θ° 
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=ax2+bx+c”κx÷αΫΜ”ΎΒψAΚΆΒψBΘ®1Θ§0Θ©Θ§”κy÷αΫΜ”ΎΒψCΘ®0Θ§3Θ©Θ§ΤδΕ‘≥Τ÷αlΈΣx=©¹1Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω Ϋ≤Δ–¥≥ωΤδΕΞΒψΉχ±ξΘΜ
Θ®2Θ©»τΕ·ΒψP‘ΎΒΎΕΰœσœόΡΎΒΡ≈ΉΈοœΏ…œΘ§Ε·ΒψN‘ΎΕ‘≥Τ÷αl…œΘ°
ΔΌΒ±PAΓΆNAΘ§«“PA=NA ±Θ§«σ¥Υ ±ΒψPΒΡΉχ±ξΘΜ
ΔΎΒ±ΥΡ±Ώ–ΈPABCΒΡΟφΜΐΉν¥σ ±Θ§«σΥΡ±Ώ–ΈPABCΟφΜΐΒΡΉν¥σ÷ΒΦΑ¥Υ ±ΒψPΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2015Ρξ4‘¬25»’14 ±11Ζ÷Θ§Ρα≤¥ΕϊΖΔ…ζ8.1ΦΕΒΊ’πΘ§’π‘¥…νΕ»20«ßΟΉΘ°÷–ΙζΨ»‘°Ε”ΜπΥΌΗœΆυ‘÷«χΨ»‘°Θ§ΧΫ≤β≥ωΡ≥Ϋ®÷ΰΈοΖœ–φœ¬ΖΫΒψC¥Π”–…ζΟϋΦΘœσΘ°‘ΎΖœ–φ“Μ≤ύΡ≥Οφ…œ―ΓΝΫΧΫ≤βΒψAΓΔBΘ§ABœύΨύ2ΟΉΘ§ΧΫ≤βœΏ”κΗΟΟφΒΡΦ–Ϋ«Ζ÷±π «30ΓψΚΆ45ΓψΘ®»γΆΦΘ©Θ° ‘»ΖΕ®…ζΟϋΥυ‘ΎΒψC”κΧΫ≤βΟφΒΡΨύάκΘ°Θ®≤ΈΩΦ ΐΨί![]() Γ÷1.41Θ§
Γ÷1.41Θ§![]() Γ÷1.73Θ©
Γ÷1.73Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com