
 如图,在△ABC中,∠ACB=90°,AC=8,sinB=
如图,在△ABC中,∠ACB=90°,AC=8,sinB=| 4 |
| 5 |
| PD |
| PQ |
| DE |
| QE |
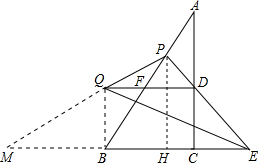 解:(1)∵在Rt△ACB中,AC=8,sinB=
解:(1)∵在Rt△ACB中,AC=8,sinB=| AC |
| AB |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| CE |
| EH |
| CD |
| PH |
| y | ||
y+6-
|
| 4 | ||
|
| 30-3x |
| x-5 |
| CE |
| BQ |
| CD |
| BE |
| y |
| 4 |
| 4 |
| 6+y |
| 30-3x |
| x-5 |
| QF |
| MB |
| PF |
| PB |
| FD |
| BE |
| PD |
| DE |
| PQ |
| QM |
| PQ |
| QE |
| PD |
| PQ |
| DE |
| QE |


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
| 得分 应聘人 项目 |
专业知识 | 英语水平 | 参加社会实践与 社团活动等 |
| 甲 | 85 | 85 | 90 |
| 乙 | 85 | 85 | 70 |
| 丙 | 80 | 90 | 70 |
| 丁 | 90 | 90 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 11 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期天 | |
| 学生奶 | 2 | 1 | 0 | 1 | 0 | 9 | 8 |
| 酸牛奶 | 70 | 70 | 80 | 75 | 85 | 80 | 100 |
| 原味奶 | 40 | 30 | 35 | 30 | 38 | 47 | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com