
 已知点O是△ABC的外心,∠A=α,求∠BOC的大小.
已知点O是△ABC的外心,∠A=α,求∠BOC的大小. 分析 这是一道推理说明:同弧所对的圆心角是圆周角的二倍;根据点O的位置分三种情况进行讨论:①当圆心O在∠BAC的内部时,如图1,②当圆心O在∠BAC的边上时,如图2,③当圆心O在∠BAC的外部时,如图3,利用外角定理和半径相等得出结论.
解答  解:分三种情况讨论:
解:分三种情况讨论:
①当圆心O在∠BAC的内部时,如图1,
过A、O作射线AD,
∵∠BOD=∠ABO+∠BAO,
∠COD=∠ACO+∠CAO,
∵OA=OB=OC,
∴∠ABO=∠BAO,∠OAC=∠OCA,
∴∠BOC=∠BOD+∠DOC=2∠BAO+2∠CAO,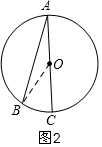
∴∠BOC=2∠BAC,
∵∠BAC=α,
∴∠BOC=2α;
②当圆心O在∠BAC的边上时,如图2,
连接OB,
∵OA=OB,
∴∠A=∠B,
∵∠BOC=∠B+∠A,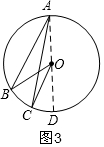
∴∠BOC=2∠A=2α;
③当圆心O在∠BAC的外部时,如图3,
过点A作直径AD,
∵OA=OB,
∴∠OAB=∠OBA,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠BOD=∠B+∠OAB,
∠COD=∠C+∠OAC,
∴∠BOC=∠BOD-∠COD=2∠OAB-2∠OAC=2∠BAC=2α.
综上所述:∠BOC=2α.
点评 在三角形的外接圆中,明确所有的半径都相等,找出圆心角和圆周角,能利用三角形证明角的大小关系的性质(①等边对等角,②三角形的一个外角等于与它不相邻的两个内角的和;)得出:①在同圆或等圆中,弧、弦、圆心角、圆周角中有一组量相等,则其他各组量都分别相等;②在同圆或等圆中,同弧所对的圆心角是圆周角的二倍.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
| 月用水量 | 不超过12吨部分 | 超过12吨不超过18吨部分 | 超过18吨部分 |
| 收费标准(元/吨) | 2.00 | 2.50 | 3.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果两个三角形全等,则它们是关于某条直线成轴对称的图形 | |
| B. | 如果两个三角形关于某条直线成轴对称,那么它们是全等三角形 | |
| C. | 等边三角形是关于一条边上的中线成轴对称的图形 | |
| D. | 一条线段是关于经过该线段中点的中线成轴对称的图形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com