
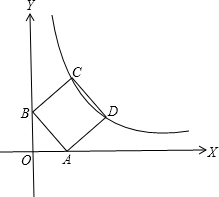
 已知如图正方形ABCD的C、D的两个顶点在双曲线y=
已知如图正方形ABCD的C、D的两个顶点在双曲线y=| 10 | x |
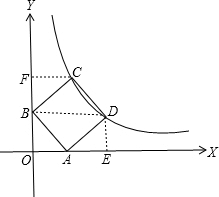 解:连接BD,过点D作DE⊥OA于E,作CF⊥y轴.
解:连接BD,过点D作DE⊥OA于E,作CF⊥y轴.| 10 |
| x |
| 10 |
| 10 |


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
| ||
| 4 |
| ||
| 4 |
| 360° |
| n |
| 90°(n-2) |
| n |
| 90°(n-2) |
| n |
| 360° |
| n |
| 90°(n-2) |
| n |
| 90°(n-2) |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
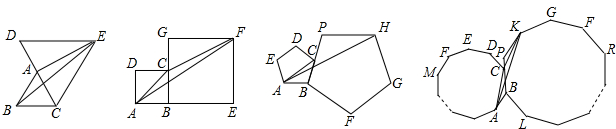
已知如图,△ABC和△DCE都是等边三角形,若△ABC的边长为1,则△BAE的面积是 .

四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是 .
……
如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
查看答案和解析>>
科目:初中数学 来源:2013届湖北省黄石市第九中学九年级下学期开学联考数学试卷(带解析) 题型:填空题
已知如图,△ABC和△DCE都是等边三角形,若△ABC的边长为1,则△BAE的面积是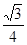 ,四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是8,……,如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
,四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是8,……,如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)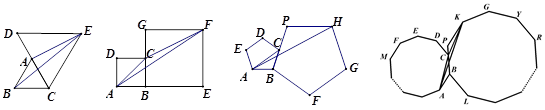
查看答案和解析>>
科目:初中数学 来源:2012-2013学年湖北省黄石市九年级下学期开学联考数学试卷(解析版) 题型:填空题
已知如图,△ABC和△DCE都是等边三角形,若△ABC的边长为1,则△BAE的面积是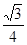 ,四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是8,……,如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
,四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是8,……,如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市通州区九年级中考一模数学卷(解析版) 题型:填空题
已知如图,△ABC和△DCE都是等边三角形,若△ABC的边长为1,则△BAE的面积是 .

四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是 .
……
如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com