
【题目】如图,![]() 是等边三角形,过它的三个顶点分别作对边的平行线,则图中共有______个等边三角形.
是等边三角形,过它的三个顶点分别作对边的平行线,则图中共有______个等边三角形.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
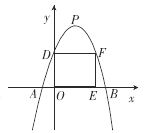
【题目】已知抛物线y=-x2+bx+c的顶点P的坐标为(n,n2+2n+1)(n≥1).
(1)求b与n,c与n之间的关系式;
(2)若抛物线y=-x2+bx+c与x轴交于点A,B(点A在点B的左边),点P到AB的距离等于线段AB长的2倍,求此抛物线y=-x2+bx+c的解析式;
(3)设抛物线y=-x2+bx+c与y轴交于点D,O为原点,矩形OEFD的顶点E,F分别在x轴和该抛物线上,当矩形OEFD的面积为20时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F.

(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD;
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
三角形的直角边长/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
阴影部分的面积/ | 398 | 392 | 382 | 368 | 350 | 302 | 272 | 200 |

(1)在这个变化过程中,自变量、因变量各是什么?
(2)请将上述表格补充完整;
(3)当等腰直角三角形的直角边长由![]() 增加到
增加到![]() 时,阴影部分的面积是怎样变化的?
时,阴影部分的面积是怎样变化的?
(4)设等腰直角三角形的直角边长为![]() ,图中阴影部分的面积为
,图中阴影部分的面积为![]() ,写出
,写出![]() 与
与![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 于点
于点![]() ,点
,点![]() 为直线
为直线![]() 上不与点
上不与点![]() 重合的一个动点.
重合的一个动点.
(1)求线段![]() 的长;
的长;
(2)当![]() 的面积是6时,求点
的面积是6时,求点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,若存在,请直接写出所有符合条件的点
全等,若存在,请直接写出所有符合条件的点![]() 的坐标,否则,说明理由.
的坐标,否则,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某政府部门进行公务员招聘考试,其中三人中录取一人,他们的成绩如下:
人 | 测试成绩 | ||
题目 | 甲 | 乙 | 丙 |
文化课知识 | 74 | 87 | 69 |
面试 | 58 | 74 | 70 |
平时表现 | 87 | 43 | 65 |
(1)按照平均成绩甲、乙、丙谁应被录取?
(2)若按照文化课知识、面试、平时表现的成绩已4:3:1的比例录取,甲、乙、丙谁应被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
查看答案和解析>>
科目:初中数学 来源: 题型:
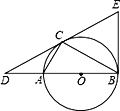
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com