
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=﹣![]() x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣![]() x+b平分矩形OABC的面积,求b的值;
x+b平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,当直线y=﹣![]() x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
(3)在(1)的条件下,将矩形OABC沿DE折叠,若点O落在边BC上,求出该点坐标;若不在边BC上,求将(1)中的直线沿y轴怎样平移,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
【答案】(1)b=12;(2)存在,DM=8﹣![]() 或DM=8+
或DM=8+![]() ;(3)沿y轴向下平移
;(3)沿y轴向下平移![]() 个单位,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
个单位,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
【解析】
试题分析:(1)根据直线y=﹣![]() x+b平分矩形OABC的面积,知道其必过矩形的中心,然后求得矩形的中心坐标为(6,3),代入解析式即可求得b值;(2)假设存在ON平分∠CNM的情况,分当直线PM与边BC和边OA相交和当直线PM与直线BC和x轴相交这两种情况,求得DM的值就存在,否则就不存在;
x+b平分矩形OABC的面积,知道其必过矩形的中心,然后求得矩形的中心坐标为(6,3),代入解析式即可求得b值;(2)假设存在ON平分∠CNM的情况,分当直线PM与边BC和边OA相交和当直线PM与直线BC和x轴相交这两种情况,求得DM的值就存在,否则就不存在;
(3)假设沿DE将矩形OABC折叠,点O落在边BC上O′处,连接PO′、OO′,得到△OPO′为等边三角形,从而得到∠OPD=30°,然后根据(2)知∠OPD>30°,得到沿DE将矩形OABC折叠,点O不可能落在边BC上;若设沿直线y=﹣![]() x+a将矩形OABC折叠,点O恰好落在边BC上O′处,连接P′O′、OO′,则有P′O′=OP′=a,在Rt△OPD和Rt△OAO′中,利用正切的定义求得a值,即可得到将矩形OABC沿直线折叠,点O恰好落在边BC上,于是得到问题的答案.
x+a将矩形OABC折叠,点O恰好落在边BC上O′处,连接P′O′、OO′,则有P′O′=OP′=a,在Rt△OPD和Rt△OAO′中,利用正切的定义求得a值,即可得到将矩形OABC沿直线折叠,点O恰好落在边BC上,于是得到问题的答案.
试题解析:(1)∵直线y=﹣![]() x+b平分矩形OABC的面积,∴其必过矩形的中心,由题意得矩形的中心坐标为(6,3),∴3=﹣
x+b平分矩形OABC的面积,∴其必过矩形的中心,由题意得矩形的中心坐标为(6,3),∴3=﹣![]() ×6+b,解得b=12;(2)假设存在ON平分∠CNM的情况,①当直线PM与边BC和边OA相交时,过O作OH⊥PM于H,∵ON平分∠CNM,OC⊥BC,∴OH=OC=6,由(1)知OP=12,∴∠OPM=30°,∴OM=OPtan30°=
×6+b,解得b=12;(2)假设存在ON平分∠CNM的情况,①当直线PM与边BC和边OA相交时,过O作OH⊥PM于H,∵ON平分∠CNM,OC⊥BC,∴OH=OC=6,由(1)知OP=12,∴∠OPM=30°,∴OM=OPtan30°=![]() ,当y=0时,由﹣
,当y=0时,由﹣![]() x+12=0解得x=8,∴OD=8,∴DM=8﹣
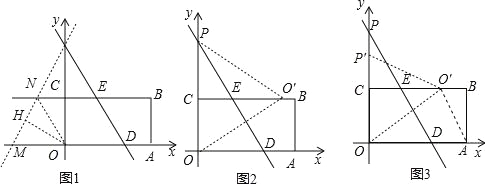
x+12=0解得x=8,∴OD=8,∴DM=8﹣![]() ;②如图1,当直线PM与直线BC和x轴相交时,同上可得OM=
;②如图1,当直线PM与直线BC和x轴相交时,同上可得OM=![]() ,OD=8,∴DM=8+
,OD=8,∴DM=8+![]() .所以存在ON平分∠CNM的情况,DM=8﹣
.所以存在ON平分∠CNM的情况,DM=8﹣![]() 或DM=8+
或DM=8+![]() ;(3)如图2假设沿DE将矩形OABC折叠,点O落在边BC上O′处连接PO′、OO′,则有PO′=OP,又由(1)得BC垂直平分OP,∴PO′=OO′,∴△OPO′为等边三角形,∴∠OPD=30°,而由(2)知∠OPD>30°,所以沿DE将矩形OABC折叠,点O不可能落在边BC上;如图3设沿直线y=﹣
;(3)如图2假设沿DE将矩形OABC折叠,点O落在边BC上O′处连接PO′、OO′,则有PO′=OP,又由(1)得BC垂直平分OP,∴PO′=OO′,∴△OPO′为等边三角形,∴∠OPD=30°,而由(2)知∠OPD>30°,所以沿DE将矩形OABC折叠,点O不可能落在边BC上;如图3设沿直线y=﹣![]() x+a将矩形OABC折叠,点O恰好落在边BC上O′处,连接P′O′、OO′,则有P′O′=OP′=a,由题意得:CP′=a﹣6,∠OPD=∠CO′O,在Rt△OPD中,tan∠OPD=
x+a将矩形OABC折叠,点O恰好落在边BC上O′处,连接P′O′、OO′,则有P′O′=OP′=a,由题意得:CP′=a﹣6,∠OPD=∠CO′O,在Rt△OPD中,tan∠OPD=![]() ,在Rt△OCO′中,tan∠CO′O=
,在Rt△OCO′中,tan∠CO′O=![]() ,∴
,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得CO′=9,在Rt△CP′O′中,由勾股定理得:(a﹣6)2+92=a2,解得a=
,解得CO′=9,在Rt△CP′O′中,由勾股定理得:(a﹣6)2+92=a2,解得a=![]() ,12﹣
,12﹣![]() =
=![]() ,所以将直线y=﹣
,所以将直线y=﹣![]() x+12沿y轴向下平移
x+12沿y轴向下平移![]() 个单位得直线y=﹣
个单位得直线y=﹣![]() x+
x+![]() ,将矩形OABC沿直线y=﹣
,将矩形OABC沿直线y=﹣![]() x+
x+![]() 折叠,点O恰好落在边BC上.
折叠,点O恰好落在边BC上.


科目:初中数学 来源: 题型:
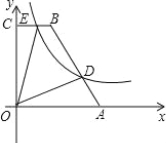
【题目】如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,双曲线y=![]() (k>0)经过点D,交BC于点E.(1)、求双曲线的解析式;(2)、求四边形ODBE的面积.
(k>0)经过点D,交BC于点E.(1)、求双曲线的解析式;(2)、求四边形ODBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批小学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了2元,结果第二批用了6600元.若商店销售这两批书包时,每个售价都是30元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】口袋内装有除颜色外完全相同的红球、白球和黑球共10个,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么黑球的个数是_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户去年承包荒山若干亩,投资7800 元改造后,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1000千克,需8 人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=1.3元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
(3)该农户加强果园管理,力争到明年纯收入达到15000元,那么纯收入增长率是多少?(纯收入=总收入﹣总支出,该农户采用了(2)中较好的出售方式出售)
查看答案和解析>>
科目:初中数学 来源: 题型:
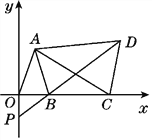
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且(a+b-3)2+|a-2b|=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)线段AO与线段AB的数量关系是______(填“>”、“≥”、“≤”、“<”或“=”);
(2)求证:△AOC≌△ABD;
(3)若∠CAD=30![]() ,当点C运动时,点P在y轴上的位置是否发生改变,为什么?
,当点C运动时,点P在y轴上的位置是否发生改变,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com