
 在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-4的图象与x轴有两个公共点.
在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-4的图象与x轴有两个公共点.分析 (1)由题意列出不等式组即可解决问题;
(2)满足条件的m的最小整数为1,由此即可解决问题.
(3)画出函数图象,利用图象法即可解决问题;
解答 解:(1)∵二次函数y=mx2-(2m+1)x+m-4的图象与x轴有两个公共点,
∴$\left\{\begin{array}{l}{m≠0}\\{[-(2m+1)]^{2}-4m(m-4)>0}\end{array}\right.$,
解得m>-$\frac{1}{20}$且m≠0,
∴m的取值范围为m>-$\frac{1}{20}$且m≠0.
(2)由题意m=1,
∴二次函数的解析式为y=x2-3x-3.
(3)∵抛物线的对称轴x=$\frac{3}{2}$,当x<$\frac{3}{2}$时,y随x的增大而减小,
∴a<1时,y1>y2,根据对称性Q(1,y2)关于对称轴的对称点为(2,y2),
观察图象可知,当a>2时,y1>y2,
综上所述,当a<1或a>2时,y1>y2.
点评 本题考查抛物线与x轴的交点、二次函数图象上的点的特征等知识,解题的关键是学会用转化的思想思考问题,学会利用图象法解决实际问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
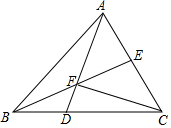 如图,D在△ABC的边BC上,DC=2BD,连接AD与△ABC的中线BE交于点F,连接CF,若△ABC的面积为24,则△AEF的面积为( )
如图,D在△ABC的边BC上,DC=2BD,连接AD与△ABC的中线BE交于点F,连接CF,若△ABC的面积为24,则△AEF的面积为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解全市九年级学生某次数学模拟考试情况,现从全市30000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
为了解全市九年级学生某次数学模拟考试情况,现从全市30000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:| 分数段 | 频数 | 频率 |
| x<60 | 20 | 0.10 |
| 60≤x<70 | 28 | 0.14 |
| 70≤x<80 | 54 | 0.27 |
| 80≤x<90 | a | 0.20 |
| 90≤x<100 | 24 | 0.12 |
| 100≤x<110 | 18 | b |
| 110≤x<120 | 16 | 0.08 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com