
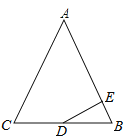
【题目】如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连接AD,由△ABC中,AB=AC=13,BC=10,D为BC中点,利用等腰三角形三线合一的性质,可证得AD⊥BC,再利用勾股定理,求得AD的长,那么在直角△ABD中根据三角函数的定义求出tan∠BAD,然后根据同角的余角相等得出∠BDE=∠BAD,于是tan∠BDE=tan∠BAD.
解:连接AD,

∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BD=![]() BC=5,
BC=5,
∴AD=![]() =12,
=12,
∴tan∠BAD=![]() =
=![]()
∵AD⊥BC,DE⊥AB,
∴∠BDE+∠ADE=90°,∠BAD+∠ADE=90°,
∴∠BDE=∠BAD,
∴tan∠BDE=tan∠BAD=![]() .
.
故选:C.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+4的图象与x轴交于B,C两点(B在C的左侧),与y轴交于点A.
x+4的图象与x轴交于B,C两点(B在C的左侧),与y轴交于点A.
(1)求出点A,B,C的坐标.
(2)在抛物线上有一动点P,抛物线的对称轴上有另一动点Q,若以B,C,P,Q为顶点的四边形是平行四边形,直接写出点P的坐标.
(3)向右平移抛物线,使平移后的抛物线恰好经过△ABC的外心,求出平移后的抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.
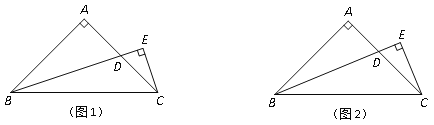
(1)若BD是AC边上的中线,如图1,求![]() 的值;
的值;
(2)若BD是∠ABC的角平分线,如图2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个测量弹跳力的体育器材,如图所示,竖杆![]() 的长度分别为200厘米和300厘米,
的长度分别为200厘米和300厘米,![]() 厘米.现有一人站在斜杆
厘米.现有一人站在斜杆![]() 下方的点
下方的点![]() 处,直立、单手上举时中指指尖(点
处,直立、单手上举时中指指尖(点![]() )到地面的高度
)到地面的高度![]() 厘米,屈膝尽力跳起时,中指指尖刚好触到斜杆的点
厘米,屈膝尽力跳起时,中指指尖刚好触到斜杆的点![]() 处,此时,就将
处,此时,就将![]() 与
与![]() 的差值
的差值![]() (厘米)作为此人此次的弹跳成绩,设
(厘米)作为此人此次的弹跳成绩,设![]() 厘米.
厘米.
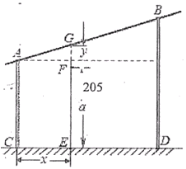
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)若他弹跳时的位置为![]() ,求该人的弹跳成绩.
,求该人的弹跳成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y1=x的图象与反比例函数![]() (k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(k≠0)的图象相交于A、B两点,点A的纵坐标为2.
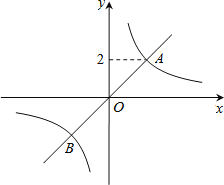
(1)求反比例函数的解析式;
(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 是等边三角形,D 为 CB 延长线上一点,E 为 BC 延长线上点.
(1)当 BD、BC 和 CE 满足什么条件时,△ADB∽△EAC?
(2)当△ADB∽△EAC 时,求∠DAE 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
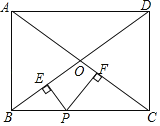
【题目】如图,在矩形ABCD中,AB=6,AD=8,P是BC上不与B和C重合的一个动点,过点P分别作BD和AC的垂线,垂足为E,F.则PE+PF的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某班同学随机投掷一枚硬币的试验结果( )
抛掷次数n | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
“正面向上”次数m | 22 | 52 | 71 | 95 | 116 | 138 | 160 | 187 | 214 | 238 |
“正面向上”频率 | 0.44 | 0.52 | 0.47 | 0.48 | 0.46 | 0.46 | 0.46 | 0.47 | 0.48 | 0.48 |
下面有三个推断:
①表中没有出现“正面向上”的概率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是( )
A. ①②B. ①③C. ③D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com