练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，△ABC中，∠CAB＝70°，在同一平面内，将△ABC绕点A旋转到△AB'C'的位置，使得C′C∥AB，则∠CAB'等于（　　）

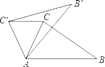
    A. 30°B. 25°C. 15°D. 10°

    【答案】A

    【解析】

    先根据平行线的性质得∠ACC′＝∠CAB＝70°，再根据旋转的性质得AC＝AC′，∠CAC′＝∠BAB′，根据等腰三角形的性质和三角形内角和计算出∠CAC′＝40°，所以∠BAB′＝40°，然后计算∠CAB′＝∠CAB﹣∠BAB′即可．

    解：∵C′C∥AB，

    ∴∠ACC′＝∠CAB＝70°，

    ∵△ABC绕点A旋转到△AB'C'的位置，

    ∴AC＝AC′，∠CAC′＝∠BAB′，

    ∴∠ACC′＝∠AC′C＝70°，

    ∴∠CAC′＝180°﹣70°﹣70°＝40°，

    ∴∠BAB′＝40°，

    ∴∠CAB′＝∠CAB﹣∠BAB′＝70°﹣40°＝30°．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AD⊥BC于D，下列条件：①∠B+∠DAC=90°；②∠B=∠DAC；③=；④AB2=BDBC．其中一定能够判定△ABC是直角三角形的有（ ）

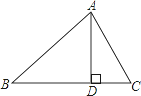
    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设是不小于的实数，关于的方程有两个不相等的实数根、，

    （1）求的取值范围；

    （2）若，求值；

    （3）求的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在矩形纸片ABCD中，AB=6，BC=8．

    （1）将矩形纸片沿BD折叠，点A落在点E处（如图①），设DE与BC相交于点F，求BF的长；

    （2）将矩形纸片折叠，使点B与点D重合（如图②），求折痕GH的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读）如图1，四边形中，，，，，经过点的直线将四边形分成两部分，直线与所成的角设为，将四边形的直角沿直线折叠，点落在点处，我们把这个操作过程记为．

    （理解）若点与点重合，则这个操作过程为[__________，__________]；

    　　　　 　　　　

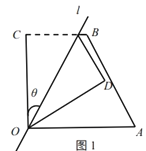
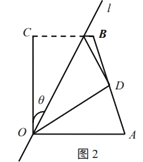
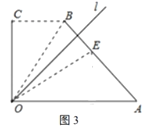
    （尝试）

    （1）若点恰为的中点(如图2)，求；

    （2）经过操作，点落在处，若点在四边形的边上(如图3)，求出的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=-x 2 +2mx-m 2+4

    (1)当m=1时，抛物线的对称轴和顶点坐标:

    (2)求证:不论m取何值时该二次函数的图像与x轴必有两个不同交点

    (3)若该二次函数的图像与x轴交于点A， B(点Ａ在点Ｂ的左侧)，顶点为C，则这时△ＡBC的面积为　　　　　

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，如果点，点为某个菱形的一组对角的顶点，且点在直线上，那么称该菱形为点的“伴随菱形”，下图为点的“伴随菱形”的一个示意图．

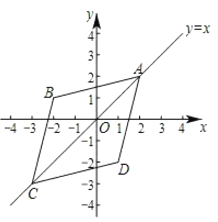
    已知点的坐标为(1，1)，点的坐标为．

    （1）点中，能够成为点的“伴随菱形”的顶点的是__________________；

    （2）如果四边形是点的“伴随菱形”．

    ①当点的坐标为时，求四边形的面积；

    ②当四边形中较小内角的度数为60°时，求四边形的面积；

    ③当四边形的面积为8，且与直线有公共点时，直接写出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示的二次函数的图象中，观察得出了下面五条信息：

    ①；②；③；④；⑤，

    你认为其中正确信息的个数有__________________个.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对x，y定义一种新运算x[]y= （其中a，b均为非零常数），这里等式右边是通常的四则混合运算，例如：0[]2= =﹣2b．已知1[]2=3，﹣1[]3=﹣2．请解答下列问题．

    (1)求a，b的值；

    (2)若M=（m2﹣m﹣1）[]（2m﹣2m2），则称M是m的函数，当自变量m在﹣1≤m≤3的范围内取值时，函数值M为整数的个数记为k，求k的值；

    查看答案和解析>>

    同步练习册答案