


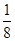 x2-
x2-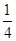 x,顶点坐标:M(1,-
x,顶点坐标:M(1,-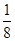 ).(2) A1(6,3).(3) t=
).(2) A1(6,3).(3) t= .
. ;
;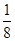 ;可分两种情况讨论:
;可分两种情况讨论: 时,设直线PQ与直线AB的交点为F,与x轴的交点为G;由题意知△FQE∽△FAG,得∠FGA=∠FEQ,由于BC∥x轴,则∠DPQ=∠FGA=∠FEQ,由此可证得△DPQ∽△DEB,DB、DE的长已求得,可用t表示出DP、DQ的长,根据相似三角形所得比例线段,即可求得此时t的值;
时,设直线PQ与直线AB的交点为F,与x轴的交点为G;由题意知△FQE∽△FAG,得∠FGA=∠FEQ,由于BC∥x轴,则∠DPQ=∠FGA=∠FEQ,由此可证得△DPQ∽△DEB,DB、DE的长已求得,可用t表示出DP、DQ的长,根据相似三角形所得比例线段,即可求得此时t的值; <t<3
<t<3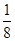 时,方法同①;
时,方法同①;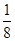 x2-
x2-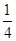 x,
x,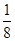 ).
).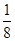 x22-
x22-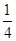 x2-
x2-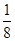 x12+
x12+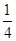 x1=3,
x1=3,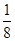 (x2+x1)-
(x2+x1)-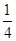 ]=3①,
]=3①,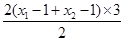 =3(x1+x2)-6,
=3(x1+x2)-6,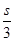 +2②,
+2②,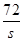 (S>0),
(S>0),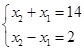 ,
, ,
,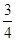 x-
x-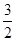 ,可得直线AB与对称轴的交点E的坐标为(1,-
,可得直线AB与对称轴的交点E的坐标为(1,-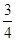 ),
),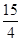 ,DP=5-t,DQ=t,
,DP=5-t,DQ=t,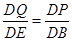 ,即
,即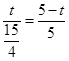 ,
, ,
, 时,如图1-1;
时,如图1-1; ,
, ,
, >
> ,
, (舍去);
(舍去); <t<3
<t<3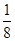 时,如图1-2;
时,如图1-2;
 ,
, ;
; 秒时,使直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.
秒时,使直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.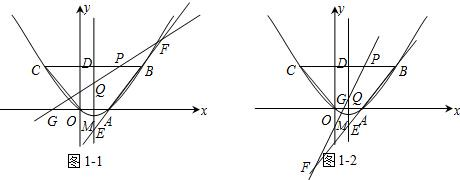


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:单选题
| A.7环 | B.8环 | C.9环 | D.10环 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com