已知,抛物线y=ax2+bx-3a经过A(-1,0)、C(0,-3)两点,与轴交于另一点B.
(1)求抛物线的解析式;
(2)已知点D与C关于抛物线的对称轴对称,求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连接DB,问在抛物线上是否存在一点M,使∠DBM=45°?若存在,求出点M的坐标;若不存在,请说明理由.
分析:(1)将A、C的坐标代入抛物线的解析式中,通过联立方程组求得该抛物线的解析式;
(2)根据(1)题所得抛物线的解析式,可确定抛物线的对称轴方程以及B、C的坐标,进而可求得D点坐标以及CD的长;由于CD∥AB,可求得∠DCB=∠OBC=∠OCB=45°(由于OB=OC=3),因此CB是∠OCD的角平分线,那么点D关于直线BC的对称点必在y轴上,过D作DD′⊥BC交y轴于D′,根据角平分线的性质可得CD′=CD,由此可求出点D′的坐标;
(3)在(2)中已经证得∠OBC=45°,若∠DBM=45°,那么∠OBM=DBC,过D作DE⊥BC于E,设直线BM交y轴于P,根据上面得到的等角,易证得△BOP∽△BED,由于△CDE是等腰Rt△,且已知CD的长,易求得CE、BE、DE的值,根据相似三角形所得比例线段,即可求得OP的值,也就得到了点P的坐标,利用待定系数法可求得直线BP的解析式,联立抛物线的解析式即可求出点M的坐标.
解答:解:(1)由题意得:将A(-1,0),C(0,-3)代入y=ax
2+bx-3a得:
,
解得
∴抛物线的解析式为y=x
2-2x-3;
(2)∵抛物线的对称轴为直线x=1,与x轴的另一个交点是B(3,0),
则点C关于抛物线对称轴的对称点D(2,-3),
∴CD=2,且CD∥AB
∵OC=OB=3,且∠COB=90°,
∴∠OCB=∠BCD=45°
过点D作DD′⊥BC交y轴于点D′,则CD′=CD=2;
∴点D′(0,-1)
即点D关于直线BC对称点的坐标为D′(0,-1);
(3)假设存在这样的点M,使∠DBM=45°,设BM交y轴于点P;
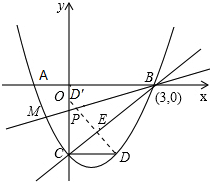
∵∠OBC=∠DBM=45°,
∴∠OBP=∠CBD;
过点D作DE⊥BC,
∵∠BCD=45°,CD=2,∴CE=DE=
,
∴BE=BC-CE=2
;
又∵∠BED=∠BOP=90°,
∴△BOP∽△BED,
∴
=,
∴OP=1.5,即P(0,-1.5);
∴直线BP的解析式为:y=
x-
;
∴抛物线与直线BP的交点M
,
解得
或
(不合题意,舍去)
∴存在这样的点M,即M(-
,-
).
点评:此题考查了二次函数解析式的确定、轴对称的性质、角平分线的性质、相似三角形的判定和性质以及函数图象交点坐标的求法等知识,综合性强,难度较大.




 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案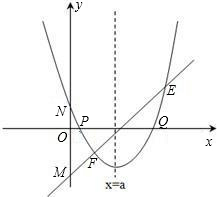 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.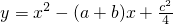 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.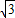 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.