
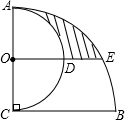
 如图,AC⊥BC,AC=BC=6,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{AB}$.过点O作BC的平行线交两弧于D、E,则阴影部分的面积是$\frac{15}{4}$π-$\frac{9\sqrt{3}}{2}$.
如图,AC⊥BC,AC=BC=6,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{AB}$.过点O作BC的平行线交两弧于D、E,则阴影部分的面积是$\frac{15}{4}$π-$\frac{9\sqrt{3}}{2}$. 分析 连接CE,如图,先利用平行线的性质得到OE⊥AC,再根据三角函数的定义求出∠OCE=60°,则OE=$\sqrt{3}$OC=3$\sqrt{3}$,然后根据扇形面积公式,利用阴影部分的面积=S扇形ACE-S扇形AOD-S△OCE进行计算即可.
解答 解:连接CE,如图,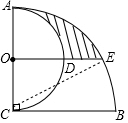
∵AC⊥BC,OE∥BC,
∴OE⊥AC,
在Rt△OCE中,OC=$\frac{1}{2}$AC=3,CE=CB=6,
∴cos∠OCE=$\frac{3}{6}$=$\frac{1}{2}$,
∴∠OCE=60°,OE=$\sqrt{3}$OC=3$\sqrt{3}$,
∴阴影部分的面积=S扇形ACE-S扇形AOD-S△OCE
=$\frac{60•π•{6}^{2}}{360}$-$\frac{90•π•{3}^{2}}{360}$-$\frac{1}{2}$×3×3$\sqrt{3}$
=$\frac{15}{4}$π-$\frac{9\sqrt{3}}{2}$.
故答案为$\frac{15π}{4}$-$\frac{9\sqrt{3}}{2}$.
点评 本题考查了扇形面积的计算:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=$\frac{n•π•{R}^{2}}{360}$或S扇形$\frac{1}{2}$lR(其中l为扇形的弧长);求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.也考查了矩形的性质.


科目:初中数学 来源: 题型:选择题
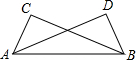 如图,已知∠CAB=∠DBA,添加一个条件使△CAB≌△DBA,以下错误的是( )
如图,已知∠CAB=∠DBA,添加一个条件使△CAB≌△DBA,以下错误的是( )| A. | ∠CBA=∠DAB | B. | ∠C=∠D | C. | AC=BD | D. | CB=DA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com