
 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.分析 (1)根据三角形中位线定理得MN=$\frac{1}{2}$AD,根据直角三角形斜边中线定理得BM=$\frac{1}{2}$AC,由此即可证明.
(2)首先证明∠BMN=90°,根据BN2=BM2+MN2即可解决问题.
解答 (1)证明:在△CAD中,∵M、N分别是AC、CD的中点,
∴MN∥AD,MN=$\frac{1}{2}$AD,
在RT△ABC中,∵M是AC中点,
∴BM=$\frac{1}{2}$AC,
∵AC=AD,
∴MN=BM.
(2)解:∵∠BAD=60°,AC平分∠BAD,
∴∠BAC=∠DAC=30°,
由(1)可知,BM=$\frac{1}{2}$AC=AM=MC,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,
∵MN∥AD,
∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,
由(1)可知MN=BM=$\frac{1}{2}$AC=1,
∴BN=$\sqrt{2}$
点评 本题考查三角形中位线定理、直角三角形斜边中线定理、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
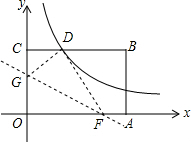 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
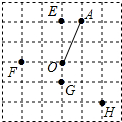
| A. | E、F、G | B. | F、G、H | C. | G、H、E | D. | H、E、F |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
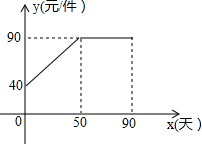 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元). | 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量p(件) | 198 | 140 | 80 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上. 查看答案和解析>>
科目:初中数学 来源: 题型:填空题
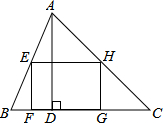 如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.
如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com