
| A. |  | B. |  | C. |  | D. |  |
科目:初中数学 来源: 题型:选择题
| A. | 了解我国东海水域是否受到日本核辐射污染 | |
| B. | 了解我们班50名同学上次月考数学成绩 | |
| C. | 了解一批节能灯泡的使用寿命 | |
| D. | 了解一批我国最新生产的核弹头的杀伤半径 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=$\frac{1}{2}$x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△ABD的面积是4.求证:四边形ABCD是矩形.
如图,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=$\frac{1}{2}$x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△ABD的面积是4.求证:四边形ABCD是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
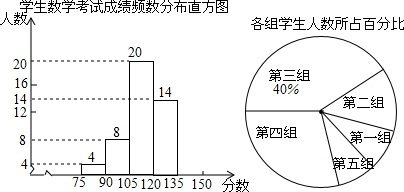
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课时间的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分),请问:
心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课时间的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分),请问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com