
����Ŀ���������ܻ��س����������Ի��ܣ�̫����6Ԫ/�裬����10Ԫ/�裮��һ�ι����������20��ʱ������20�貿�ֵ����۸��8�ۣ�
(1)�ֱ�д�����ֻ��ܵĸ�����y(Ԫ)���ڹ�����x(��)�ĺ�������ʽ��
(2)Ϊ��������������С���ƻ����û��ع��������ֻ��ܹ�90�裬����̫������������������������һ�룮���ֻ��ܸ��������ʱ���ܷ������٣������ܷ����Ƕ���Ԫ��
���𰸡���1��y=![]() ��2��̫����30��������60��ʱ���ܷ������������ٷ�����700Ԫ
��2��̫����30��������60��ʱ���ܷ������������ٷ�����700Ԫ
��������
����(1)��̫�����ļ۸�=6�����������ļ۸��x��20��x��20��������ֱ���м��㣬�ó���������ʽ��(2)��������̫������������m�裬������������(90-m)�裬�������ֻ����ܷ�����wԪ�������������m��ȡֵ��Χ��Ȼ��ó�w��m�ĺ�����ϵʽ��Ȼ�����һ�κ����������Եó���Сֵ.
���������(1)��y̫����=6x��
��y����=10x��x��20����
��y����=10��20+10��0.8����x-20��=200+8x-160=8x+40��x��20��
(2)���������⣬ ��̫������������m�裬������������(90-m)�裬�������ֻ����ܷ�����wԪ��
��m��![]() (90-m) ��m��30��
(90-m) ��m��30��
��w=6m+[8��90-m��+40]=760-2m
��-2��0 ��w����m���������С�� ����m=30ʱ��
w��С=760-2��30=700��Ԫ����
��̫����30�裬����60��ʱ���ܷ������٣����ٷ�����700Ԫ��


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������У�������Ϊ�ж���ABD�ա�BAC�������ǣ� )

A. ��D����C����BAD����ABC B. ��BAD����ABC����ABD����BAC
C. BD��AC����BAD����ABC D. AD��BC��BD��AC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����λ������λ����![]() ��ʮλ����
��ʮλ����![]() ����λ����
����λ����![]() �����ǿ��Լ���
�����ǿ��Լ���![]() ��
�� ![]() ��ʾ������
��ʾ������![]() ��������������ӣ�
��������������ӣ�
��1��![]() ������ ��ʾ��
������ ��ʾ��
��2��![]() ������ ��ʾ��
������ ��ʾ��
��3��ŷ����ʦ��4Ϊͬѧ��һ��������Ϸ������Aͬѧ������һ����λ�������������λ����ֽ��д���鹹��һ����λ������Bͬѧ���������������789����ô����ֽ��д�ľ���789789��B�������λ������7���õ�����д����һ��ֽ�ϲ�����Cͬѧ��Cͬѧ��Bͬѧ���������ֳ���11���õ�����д����һ��ֽ�ϲ�����Dͬѧ��Dͬѧ��Cͬѧ���������ֳ���13���õ�����д����һ��ֽ�ϣ���������Aͬѧ������![]() ͬѧ�����ֺ����տ�ʼ���������ʲô��ϵ����˵������.
ͬѧ�����ֺ����տ�ʼ���������ʲô��ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
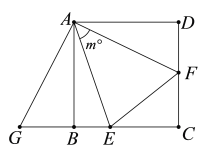
����Ŀ����ͼ����֪������![]() �ı߳���
�ı߳���![]() ��
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת���������߷ֱ�
˳ʱ����ת���������߷ֱ�![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ӳ�����һ�㣬��ʼ�ձ���
�ӳ�����һ�㣬��ʼ�ձ���![]() ��
��
��1����֤��![]() ��
��
��2����֤��![]() ��
��
��3����![]() ʱ��
ʱ��
����![]() ��ֵ������
��ֵ������![]() ��
��![]() ���е㣬��
���е㣬��![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
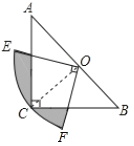
����Ŀ����ͼ������ABC�У���C=90�㣬AC=BC��б��AB=2��O��AB���е㣬��OΪԲ�ģ��߶�OC�ij�Ϊ�뾶��Բ�Ľ�Ϊ90��������OEF����EF������C����ͼ����Ӱ���ֵ����Ϊ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����淽������һ���ı���ABCD�͵�O�����ڷ����л�������ͼ��(ֻҪ��ƽ�ơ���ת���ͼ������Ҫ��д����ͼ�������)��
(1)�����ı���ABCD�Ե�OΪ��ת��������ʱ����ת90����õ����ı���A1B1C1D1��
(2)�����ı���A1B1C1D1����ƽ��3��(3��С����ı߳�)��õ����ı���A2B2C2D2��
(3)��գ���ÿ��С����ı߳�Ϊ1�����ı���A1B1C1D1���ı���A2B2C2D2�ص����ֵ����Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ����Ĵ�ֱƽ���߷ֱ�AB��BD��BC�ڵ�E��F��G������ED��DG��
��1�����ж��ı���EBGD����״����˵�����ɣ�
��2������ABC=30�㣬��C=45�㣬ED=2![]() ����H��BD�ϵ�һ�����㣬��HG+HC����Сֵ��
����H��BD�ϵ�һ�����㣬��HG+HC����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
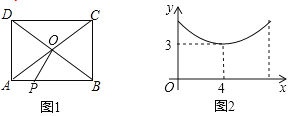
����Ŀ����ͼ1���ڳ�����![]() �У��Խ���
�У��Խ���![]() ��
��![]() ���ڵ�O������P�ӵ�A��������
���ڵ�O������P�ӵ�A��������![]() �����˶��������Bʱֹͣ�����P���ߵ�·��Ϊx���߶�
�����˶��������Bʱֹͣ�����P���ߵ�·��Ϊx���߶�![]() �ij�Ϊy����y��x֮��ĺ���ͼ����ͼ2��ʾ��ͼ����y��Ľ���ΪE����E��������Ϊ_______________������
�ij�Ϊy����y��x֮��ĺ���ͼ����ͼ2��ʾ��ͼ����y��Ľ���ΪE����E��������Ϊ_______________������![]() ���ܳ�Ϊ____________��
���ܳ�Ϊ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��0��a����B��b��a������a��b���㣨a��3��2+|b��6|��0����ͬʱ����A��B�ֱ�����ƽ��3����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��AB��

��1�����C��D�����꼰�ı���ABDC�����S�ı���ABCD��
��2����y�����Ƿ����һ��M������MC��MD��ʹS��MCD��![]() S�ı���ABCD������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
S�ı���ABCD������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
��3����P��ֱ��BD�ϵ�һ�����㣬����PA��PO������P��BD���ƶ�ʱ������B��D�غϣ���ֱ��д����BAP����DOP����APO֮�������������ϵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com