
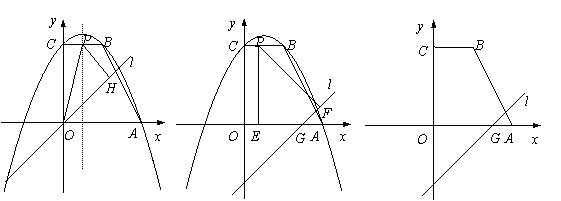
��ͼ��ֱ������ABCO������OA,OC����������������ϣ�BC��x�ᣬOA=OC=4����ֱ��x=1Ϊ�Գ���������߹�A,B,C����.
��1����������ߵĺ�������ʽ.
��2����ֱ֪��l�Ľ���ʽΪy=x+m������x�ύ�ڵ�G��������ABCO��һ����ȡ��P.
�ٵ�m=0ʱ����ͼ1����P�������߶Գ�����BC�Ľ��㣬����P��PH��ֱ��l�ڵ�H,����OP,�����OPH�����.
 �ڵ�m=-3ʱ������P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����Ϊ��E,F.�Ƿ���������ĵ�P,ʹ��P,E,FΪ������������ǵ���������?�����ڣ������P�����ꣻ�������ڣ���˵������.
�ڵ�m=-3ʱ������P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����Ϊ��E,F.�Ƿ���������ĵ�P,ʹ��P,E,FΪ������������ǵ���������?�����ڣ������P�����ꣻ�������ڣ���˵������.
|
 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ͨ������ͶƱѡ����һ��������Т�ĵ������ꡱ�����ݸ�����������ѡ�������������ͳ�Ʊ����������֣�ͳ�Ʊ���ǰ���е��������ݶ�����ȷ�ģ�����������һ�������Ǵ���ģ���ش��������⣺
��1��ͳ�Ʊ���a=��0.1����b=��6����
��2��ͳ�Ʊ�����������һ�������Ǵ���ģ������ݵ���ȷֵ�Ƕ��٣�
��3�������о��������������ص�4λ������Т�ĵ������ꡱ�У���ѡ��λ��Ϊ�м���������ˣ�A��B�������ء�����Т�ĵ������ꡱ�е���λ����A��Bͬʱ��ѡ�ĸ����Ƕ��٣�
| ���� | Ƶ�� | Ƶ�� |
| ������ | 4 | a |
| ������ | 5 | 0.125 |
| ���� | b | 0.15 |
| ������ | 8 | 0.2 |
| ������ | 5 | 0.125 |
| ������� | 12 | 0.25 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�������н�����ͼ��ʾ��ֱ������ϵ����������A��O��B��λ����ͼ,���ǵ�����ֱ���(-1,1),(0,0)��(1,0).
��1����ͼ2����������C��ʹA��O��B�� C�Ŀ����ӳ�Ϊһ����Գ�ͼ�Σ�����ͼ �л�����ͼ�εĶԳ���.
��2�����������λ������һ������P��ʹA,O,B,P�Ŀ����ӳ�Ϊһ����Գ�ͼ�Σ���ֱ��д������P��λ�õ�����.��д��2�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij�����������ͼ������ͼ����ͼ�ֱ���ͼ����ü���������Ϊ��������
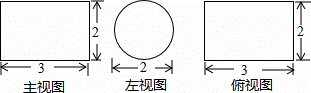
| �� | A�� | 3�� | B�� | 2�� | C�� | �� | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪һ�κ���y=��1��m��x+m��2����m�� ___________��ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����������ȷ���ǣ�������
| �� | A�� | a2+a3=a5 | B�� | ��﹣2a2��3=﹣6a6 | C�� | ��2a+1����2a﹣1��=2a2﹣1 | D�� | ��2a3﹣a2����a2=2a﹣1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ijУ��֯������Ϊ�����ڼ��Լ��Ϊʱ�С��ĵ���С����Ʒ��������ִ��������ȡ������Ʒ����A��B��C��D�ĸ��ȼ��������ۣ������ݽ������������������������ͳ��ͼ��
��1�����ȡ�˶��ٷ���Ʒ��
��2���˴γ�ȡ����Ʒ�еȼ�ΪB����Ʒ����48��������ȫ����ͳ��ͼ��
��3������У��������800����Ʒ������Ƶȼ�ΪA����ƷԼ�ж��ٷݣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com