
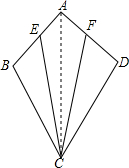
 在一个风筝ABCD中,AB=AD,BC=DC
在一个风筝ABCD中,AB=AD,BC=DC| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n |
 ①证明:如图,连结AC.
①证明:如图,连结AC.
|
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 3 |
| 1 |
| 3 |
|
| 1 |
| 3 |
| 1 |
| 3 |
|
| 1 |
| 4 |
| 1 |
| 4 |
|
| 1 |
| 4 |
| 1 |
| 4 |
|
| 1 |
| n |
| 1 |
| n |


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com