
【题目】如图,AB为⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A重合),过点P作AB的垂线交BC于点Q. 
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
(2)若cosB= ![]() ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.
【答案】
(1)解:CD与⊙O相切.理由如下:
连结OC,如图,

∵OC=OB,
∴∠2=∠B,
∵DQ=DC,
∴∠1=∠Q,
∵QP⊥PB,
∴∠BPQ=90°,
∴∠Q+∠B=90°,
∴∠1+∠2=90°,
∴∠DCO=180°﹣∠1﹣∠2=90°,
∴OC⊥CD,
而OC为⊙O的半径,
∴CD为⊙O的切线;
(2)解:连接AC,如图,

∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,cosB= ![]() =
= ![]() =
= ![]() ,
,
而BP=6,AP=1,
∴BC= ![]() ,
,
在Rt△BPQ中,cosB= ![]() =
= ![]() ,
,
∴BQ= ![]() =10,
=10,
∴QC=BQ﹣BC=10﹣ ![]() =
= ![]() .
.
【解析】(1)连结OC,由OC=OB得∠2=∠B,DQ=DC得∠1=∠Q,根据QP⊥PB得到∠Q+∠B=90°,则∠1+∠2=90°,再利用平角的定义得到∠DCO=90°,然后根据切线的判定定理得到CD为⊙O的切线;(2)连结AC,由AB为⊙O的直径得∠ACB=90°,根据余弦的定义得cosB= ![]() =
= ![]() =
= ![]() ,可计算出BC=
,可计算出BC= ![]() ,在Rt△BPQ中,利用余弦的定义得cosB=
,在Rt△BPQ中,利用余弦的定义得cosB= ![]() =
= ![]() ,可计算出BQ=10,然后利用QC=BQ﹣BC进行计算即可.
,可计算出BQ=10,然后利用QC=BQ﹣BC进行计算即可.
【考点精析】关于本题考查的切线的判定定理和解直角三角形,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP. 
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):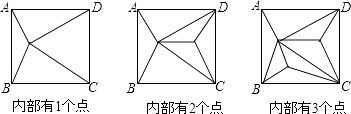
(1)填写如表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是( ) 
A.AB=AD
B.AC=BD
C.AD=BC
D.AB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4 ![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( ) 
A.1
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D. 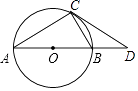
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB= ![]() CD,求⊙O半径.
CD,求⊙O半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2 ![]() ,则∠A=( )
,则∠A=( ) 
A.120°
B.100°
C.60°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( ) 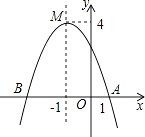
A.a<0
B.当x=﹣1时,函数y有最小值4
C.对称轴是直线=﹣1
D.点B的坐标为(﹣3,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com