
 如图,四边形ABCD各顶点的坐标分别是A(0,0),B(8,0),C(6,4),D(3,6),求出四边形ABCD的面积.
如图,四边形ABCD各顶点的坐标分别是A(0,0),B(8,0),C(6,4),D(3,6),求出四边形ABCD的面积. 分析 本题应利用分割法,把四边形分割成两个三角形加上一个梯形后再求面积.
解答 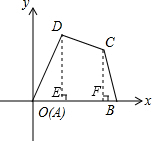 解:过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:
解:过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:
S=S△OED+SEFCD+S△CFB
=$\frac{1}{2}$×AE×DE+$\frac{1}{2}$×(CF+DE)×EF+$\frac{1}{2}$×FC×FB.
=$\frac{1}{2}$×3×6+$\frac{1}{2}$×(4+6)×3+$\frac{1}{2}$×2×4
=28.
故四边形ABCD的面积为28.
点评 此题主要考查了点的坐标的意义以及与图形相结合的具体运用.要掌握两点间的距离公式和图形有机结合起来的解题方法.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | y=2(x+2)2+3 | B. | y=2(x-2)2-3 | C. | y=2(x+2)2-3 | D. | y=2(x-2)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
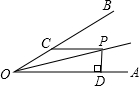 如图所示,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PC=4,则PD的长为( )
如图所示,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PC=4,则PD的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com