解:(1)∵⊙P和x轴相切时,⊙P的半径为1,
∴点P的纵坐标为1,
当y=1时,

=1,
解得x=3,
所以,点P的坐标是(3,1),
所以,方程的解是x=3;
(2)由(1)可知,点P(3,1),
又∵抛物线y=ax
2+bx的对称轴为x=1,
∴
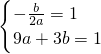
,
解得
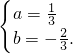
所以,抛物线的解析式为y=

x
2-

x,
令

x
2-

x=0,
解得x
1=0,x
2=2,
所以,点A(2,0);
(3)∵点P(3,1)在抛物线上,
∴9a+3b=1,
a=
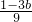
,
∵b<0,
∴-b>0,
∴1-3b>1,
∴a>

,
∵

<

,
∴a的值不能为

.
分析:(1)根据⊙P和x轴相切可知点P的纵坐标是1,代入抛物线解析式求出x的值,即可得到点P的坐标,然后根据方程的解即为点P的横坐标解答;
(2)根据对称轴解析式与点A的坐标得到关于a、b的二元一次方程组,解方程组求出a、b的值,即可得到抛物线解析式,然后令y=0,解关于x的一元二次方程即可得到点A的坐标;
(3)把点P的坐标代入抛物线,然后用b表示出a,再根据b<0判断出a的取值范围,即可进行判断.
点评:本题是二次函数综合题型,主要涉及直线与圆相切,利用图象的交点求方程的解,待定系数法求二次函数解析式,以及抛物线与x轴的交点问题,都是基本应用,难度不大.

 ,点P为第一象限分支上一动点,以P为圆心1为半径画圆,当
,点P为第一象限分支上一动点,以P为圆心1为半径画圆,当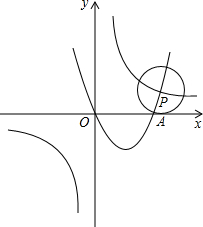 ⊙P和x轴相切时,抛物线y=ax2+bx(a>0,b<0)与y=
⊙P和x轴相切时,抛物线y=ax2+bx(a>0,b<0)与y= 的图象交于点P,与x轴交于A点.根据所给条件,解答下列问题:
的图象交于点P,与x轴交于A点.根据所给条件,解答下列问题: =0的解为________;
=0的解为________; .
. =1,
=1,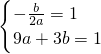 ,
,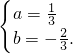
 x2-
x2- x,
x, x2-
x2- x=0,
x=0,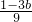 ,
, ,
, <
< ,
, .
.

 如图,已知函数y1=kx+b与函数y2=
如图,已知函数y1=kx+b与函数y2= 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于