
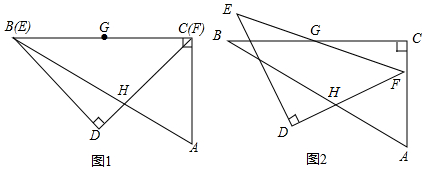
分析 如图1中,作HM⊥BC于M,设HM=CM=a.在Rt△BHM中,BH=2HM=2a,BM=$\sqrt{3}$a,根据BM+MF=BC,可得$\sqrt{3}$a+a=12,推出a=6$\sqrt{3}$-6,推出BH=2a=12$\sqrt{3}$-12.如图2中,当DG⊥AB时,易证GH1⊥DF,此时BH1的值最小,易知BH1=BK+KH1=3$\sqrt{3}$+3,当旋转角为60°时,F与H2重合,易知BH2=6$\sqrt{3}$,观察图象可知,在∠CGF从0°到60°的变化过程中,点H相应移动的路径长=2HH1+HH2,由此即可解决问题.
解答 解:如图1中,作HM⊥BC于M,设HM=a,则CM=HM=a.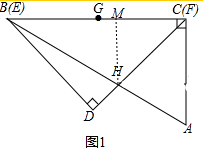
在Rt△ABC中,∠ABC=30°,BC=12,
在Rt△BHM中,BH=2HM=2a,BM=$\sqrt{3}$a,
∵BM+FM=BC,
∴$\sqrt{3}$a+a=12,
∴a=6$\sqrt{3}$-6,
∴BH=2a=12$\sqrt{3}$-12.
如图2中,当DG⊥AB时,易证GH1⊥DF,此时BH1的值最小,易知BH1=BK+KH1=3$\sqrt{3}$+3,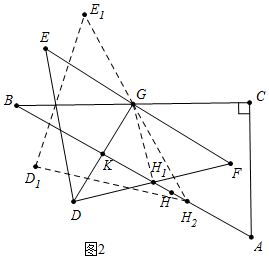
∴HH1=BH-BH1=9$\sqrt{3}$-15,
当旋转角为60°时,F与H2重合,易知BH2=6$\sqrt{3}$,
观察图象可知,在∠CGF从0°到60°的变化过程中,点H相应移动的路径长=2HH1+HH2=18$\sqrt{3}$-30+[6$\sqrt{3}$-(12$\sqrt{3}$-12)]=12$\sqrt{3}$-18.
故答案为(12$\sqrt{3}$-12)cm,(12$\sqrt{3}$-18)cm.
点评 本题考查轨迹、旋转变换、解直角三角形、锐角三角函数等知识,解题的关键是正确寻找点H的运动轨迹,属于中考常考题型.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
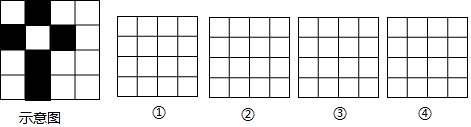
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
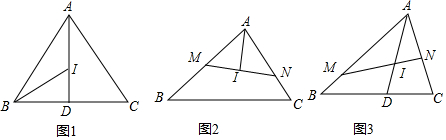
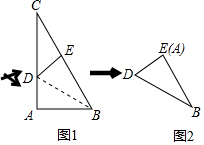 在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.
在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
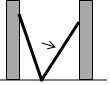 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )| A. | 0.7米 | B. | 1.5米 | C. | 2.2米 | D. | 2.4米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.6553×108 | B. | 1.6553×1011 | C. | 1.6553×1012 | D. | 1.6553×1013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com