已知一元二次方程2x2-5x+k=0有实数根,则满足条件的所有正整数k的方差为 .
【答案】
分析:根据一元二次方程ax
2+bx+c=0(a≠0)的根的判别式△=b
2-4ac的意义得到△≥0,即5
2-4×2×k≥0,解不等式得到满足条件的正整数为1、2、3,然后根据方差的定义计算即可.
解答:解:∵一元二次方程2x
2-5x+k=0有实数根,
∴△≥0,即5
2-4×2×k≥0,解得k≤
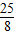
,
当k为正整数时,k取1、2、3.
数据1、2、3,它的平均数等于2,
∴S=

[(1-2)
2+(2-2)
2+(3-2)
2]=

.
故答案为

.
点评:本题考查了一元二次方程ax
2+bx+c=0(a≠0)的根的判别式△=b
2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了方差的定义.

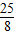 ,
, [(1-2)2+(2-2)2+(3-2)2]=
[(1-2)2+(2-2)2+(3-2)2]= .
. .
.
