
【题目】以直线![]() 上点
上点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将直角
,将直角![]() 的直角顶点放在点
的直角顶点放在点![]() 处.
处.
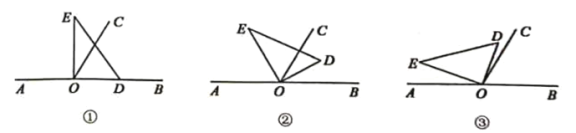
(1)若直角![]() 的边
的边![]() 在射线
在射线![]() 上(图①),求
上(图①),求![]() 的度数;
的度数;
(2)将直角![]() 绕点
绕点![]() 按逆时针方向转动,使得
按逆时针方向转动,使得![]() 所在射线平分
所在射线平分![]() (图②),说明
(图②),说明![]() 所在射线是
所在射线是![]() 的平分线;
的平分线;
(3)将直角![]() 绕点
绕点![]() 按逆时针方向转动到某个位置时,恰好使得
按逆时针方向转动到某个位置时,恰好使得![]() (图③),求
(图③),求![]() 的度数.
的度数.
【答案】(1)![]() ;(2)见解析; (3)
;(2)见解析; (3) ![]() 或
或![]()
【解析】
(1)代入∠BOE=∠COE+∠COB求出即可;
(2)求出∠AOE=∠COE,根据∠DOE=90°求出∠AOE+∠DOB=90°,∠COE+∠COD=90°,推出∠COD=∠DOB,即可得出答案;
(3)要分情况讨论,一种是∠COD在∠BOC的内部,另一种是∠COD在∠BOC的外部,再根据平角等于180°可通过列方程求出即可.
解:(1)∵![]() ,
,
又∵![]() ,
,
∴![]() .
.
(2)∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 所在直线是
所在直线是![]() 的平分线.
的平分线.
(3)设![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,
①若∠COD在∠BOC的外部,
∴![]() ,解得x=10,
,解得x=10,
∴∠COD=10°,
∴∠BOD=60°+10°=70°;
②若∠COD在∠BOC的内部,
![]() ,解得x=30,
,解得x=30,
∴∠COD=30°,
∴∠BOD=60°-30°=30°;
即![]() 或
或![]() ,
,
∴![]() 或
或![]() .
.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】将一副三角板的两个锐角顶点重合,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的平分线.
的平分线.
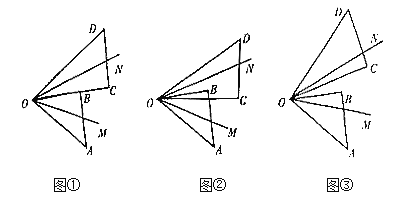
(1)如图①所示,当![]() 与
与![]() 重合时,则
重合时,则![]() 的大小为______.
的大小为______.
(2)当![]() 绕着点
绕着点![]() 旋转至如图②所示,当
旋转至如图②所示,当![]() ,则
,则![]() 的大小为多少?
的大小为多少?
(3)当![]() 绕着点
绕着点![]() 旋转至如图③所示,当
旋转至如图③所示,当![]() 时,求
时,求![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司有甲、乙、丙三个机器人分配快件,甲单独完成需要x小时,乙单独完成需要y小时,丙单独完成需要z小时.
(1)求甲单独完成的时间是乙丙合作完成时间的几倍?
(2)若甲单独完成的时间是乙丙合作完成时间的a倍,乙单独完成的时间是甲丙合作完成时间的b倍,丙单独完成的时间是甲乙合作完成时间的c倍,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=kx2+(k﹣2)x﹣2(其中k>0).
(1)求该抛物线与x轴的交点及顶点的坐标(可以用含k的代数式表示);
(2)若记该抛物线顶点的坐标为P(m,n),直接写出|n|的最小值;
(3)将该抛物线先向右平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
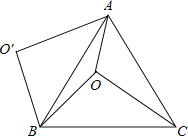
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO![]() ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,且
,且![]() G为线段
G为线段![]() 上一点,
上一点,![]() 两点分别从
两点分别从![]() 点沿
点沿![]() 方向同时运动,设
方向同时运动,设![]() 点的运动速度为
点的运动速度为![]() 点的运动速度为
点的运动速度为![]() ,运动时间为
,运动时间为![]() .
.
(1)![]() 点对应的数为 ,
点对应的数为 ,![]() 点对应的数为 ;
点对应的数为 ;
(2)若![]() ,试求
,试求![]() 为多少
为多少![]() 时,
时,![]() 两点的距离为
两点的距离为![]() ;
;
(3)若![]() ,点
,点![]() 为数轴上任意一点,且
为数轴上任意一点,且![]() ,请直接写出
,请直接写出![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设(a,b)是一次函数y=(k-2)x+m与反比例函数![]() 的图象的交点,且a、b是关于x的一元二次方程
的图象的交点,且a、b是关于x的一元二次方程![]() 的两个不相等的实数根,其中k为非负整数,m、n为常数.
的两个不相等的实数根,其中k为非负整数,m、n为常数.
(1)求k的值;
(2)求一次函数与反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤.设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y元,求y与x的函数关系式;
(2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com