
í╛╠Γ─┐í┐┼╫╬∩╧▀yú╜x2+bx+c╛¡╣²╡πAíóBíóCú¼╥╤╓¬Aú¿⌐ü1ú¼0ú⌐ú¼Cú¿0ú¼⌐ü3ú⌐ú«
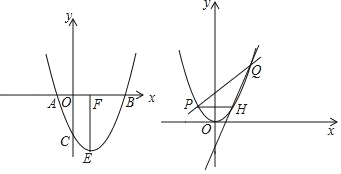
ú¿1ú⌐╟≤┼╫╬∩╧▀╡─╜Γ╬÷╩╜ú╗
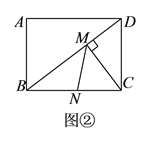
ú¿2ú⌐╚τ═╝1ú¼┼╫╬∩╧▀╢Ñ╡π╬¬Eú¼EFí═x╓ß╙┌F╡πú¼Mú¿mú¼0ú⌐╩╟x╓ß╔╧╥╗╢»╡πú¼N╩╟╧▀╢╬EF╔╧╥╗╡πú¼╚⌠í╧MNCú╜90íπú¼╟δ╓╕│÷╩╡╩²m╡─▒Σ╗»╖╢╬ºú¼▓ó╦╡├≈└φ╙╔ú«
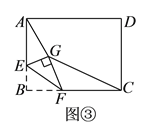
ú¿3ú⌐╚τ═╝2ú¼╜½┼╫╬∩╧▀╞╜╥╞ú¼╩╣╞Σ╢Ñ╡πE╙δ╘¡╡πO╓╪║╧ú¼╓▒╧▀yú╜kx+2ú¿kú╛0ú⌐╙δ┼╫╬∩╧▀╧α╜╗╙┌╡πPíóQú¿╡πP╘┌╫≤▒▀ú⌐ú¼╣²╡πP╫≈x╓ß╞╜╨╨╧▀╜╗┼╫╬∩╧▀╙┌╡πHú¼╡▒k╖ó╔·╕─▒Σ╩▒ú¼╟δ╦╡├≈╓▒╧▀QH╣²╢¿╡πú¼▓ó╟≤╢¿╡π╫°▒Ωú«
í╛┤≡░╕í┐ú¿1ú⌐yú╜x2⌐ü2x⌐ü3ú╗ú¿2ú⌐![]() ú╗ú¿3ú⌐╡▒k╖ó╔·╕─▒Σ╩▒ú¼╓▒╧▀QH╣²╢¿╡πú¼╢¿╡π╫°▒Ω╬¬ú¿0ú¼⌐ü2ú⌐
ú╗ú¿3ú⌐╡▒k╖ó╔·╕─▒Σ╩▒ú¼╓▒╧▀QH╣²╢¿╡πú¼╢¿╡π╫°▒Ω╬¬ú¿0ú¼⌐ü2ú⌐
í╛╜Γ╬÷í┐
ú¿1ú⌐░╤╡πAú¿⌐ü1ú¼0ú⌐ú¼Cú¿0ú¼⌐ü3ú⌐┤·╚δ┼╫╬∩╧▀▒φ┤∩╩╜╟≤╡├bú¼cú¼╝┤┐╔╡├│÷┼╫╬∩╧▀╡─╜Γ╬÷╩╜ú╗
ú¿2ú⌐╫≈CHí═EF╙┌Hú¼╔ΦN╡─╫°▒Ω╬¬ú¿1ú¼nú⌐ú¼╓ñ├≈Rtí≈NCHí╫í≈MNFú¼┐╔╡├mú╜n2+3n+1ú¼╥≥╬¬⌐ü4í▄ní▄0ú¼╝┤┐╔╡├│÷m╡─╚í╓╡╖╢╬ºú╗
ú¿3ú⌐╔Φ╡πPú¿x1ú¼y1ú⌐ú¼Qú¿x2ú¼y2ú⌐ú¼╘≥╡πHú¿⌐üx1ú¼y1ú⌐ú¼╔Φ╓▒╧▀HQ▒φ┤∩╩╜╬¬yú╜ax+tú¼╙├┤²╢¿╧╡╩²╖¿║═╬ñ┤∩╢¿└φ┐╔╟≤╡├aú╜x2⌐üx1ú¼tú╜⌐ü2ú¼╝┤┐╔╡├│÷╓▒╧▀QH╣²╢¿╡πú¿0ú¼⌐ü2ú⌐ú«
╜Γú║ú¿1ú⌐í▀┼╫╬∩╧▀yú╜x2+bx+c╛¡╣²╡πAíóCú¼
░╤╡πAú¿⌐ü1ú¼0ú⌐ú¼Cú¿0ú¼⌐ü3ú⌐┤·╚δú¼╡├ú║![]() ú¼
ú¼
╜Γ╡├![]() ú¼
ú¼
íα┼╫╬∩╧▀╡─╜Γ╬÷╩╜╬¬yú╜x2⌐ü2x⌐ü3ú╗
ú¿2ú⌐╚τ═╝ú¼╫≈CHí═EF╙┌Hú¼
í▀yú╜x2⌐ü2x⌐ü3ú╜ú¿x⌐ü1ú⌐2⌐ü4ú¼
íα┼╫╬∩╧▀╡─╢Ñ╡π╫°▒ΩEú¿1ú¼⌐ü4ú⌐ú¼
╔ΦN╡─╫°▒Ω╬¬ú¿1ú¼nú⌐ú¼⌐ü4í▄ní▄0
í▀í╧MNCú╜90íπú¼
íαí╧CNH+í╧MNFú╜90íπú¼
╙╓í▀í╧CNH+í╧NCHú╜90íπú¼
íαí╧NCHú╜í╧MNFú¼
╙╓í▀í╧NHCú╜í╧MFNú╜90íπú¼
íαRtí≈NCHí╫í≈MNFú¼
íα![]() ú¼╝┤
ú¼╝┤![]()
╜Γ╡├ú║mú╜n2+3n+1ú╜![]() ú¼
ú¼
íα╡▒![]() ╩▒ú¼m╫ε╨í╓╡╬¬
╩▒ú¼m╫ε╨í╓╡╬¬![]() ú╗
ú╗
╡▒nú╜⌐ü4╩▒ú¼m╙╨╫ε┤≤╓╡ú¼m╡─╫ε┤≤╓╡ú╜16⌐ü12+1ú╜5ú«
íαm╡─╚í╓╡╖╢╬º╩╟![]() ú«
ú«
ú¿3ú⌐╔Φ╡πPú¿x1ú¼y1ú⌐ú¼Qú¿x2ú¼y2ú⌐ú¼
í▀╣²╡πP╫≈x╓ß╞╜╨╨╧▀╜╗┼╫╬∩╧▀╙┌╡πHú¼
íαHú¿⌐üx1ú¼y1ú⌐ú¼
í▀yú╜kx+2ú¼yú╜x2ú¼
╧√╚Ñy╡├ú¼x2⌐ükx⌐ü2ú╜0ú¼
x1+x2ú╜kú¼x1x2ú╜⌐ü2ú¼
╔Φ╓▒╧▀HQ▒φ┤∩╩╜╬¬yú╜ax+tú¼
╜½╡πQú¿x2ú¼y2ú⌐ú¼Hú¿⌐üx1ú¼y1ú⌐┤·╚δú¼╡├![]() ú¼
ú¼
íαy2⌐üy1ú╜aú¿x1+x2ú⌐ú¼╝┤kú¿x2⌐üx1ú⌐ú╜kaú¼
íαaú╜x2⌐üx1ú¼
í▀![]() ú╜ú¿ x2⌐üx1ú⌐x2+tú¼
ú╜ú¿ x2⌐üx1ú⌐x2+tú¼
íαtú╜⌐ü2ú¼
íα╓▒╧▀HQ▒φ┤∩╩╜╬¬yú╜ú¿ x2⌐üx1ú⌐x⌐ü2ú¼
íα╡▒k╖ó╔·╕─▒Σ╩▒ú¼╓▒╧▀QH╣²╢¿╡πú¼╢¿╡π╫°▒Ω╬¬ú¿0ú¼⌐ü2ú⌐ú«


 ╚²╨┬┐∞│╡╜≡┼╞╓▄╓▄┴╖╧╡┴╨┤≡░╕
╚²╨┬┐∞│╡╜≡┼╞╓▄╓▄┴╖╧╡┴╨┤≡░╕
| ─Ω╝╢ | ╕▀╓╨┐╬│╠ | ─Ω╝╢ | │⌡╓╨┐╬│╠ |
| ╕▀╥╗ | ╕▀╥╗├Γ╖╤┐╬│╠═╞╝÷úí | │⌡╥╗ | │⌡╥╗├Γ╖╤┐╬│╠═╞╝÷úí |
| ╕▀╢■ | ╕▀╢■├Γ╖╤┐╬│╠═╞╝÷úí | │⌡╢■ | │⌡╢■├Γ╖╤┐╬│╠═╞╝÷úí |
| ╕▀╚² | ╕▀╚²├Γ╖╤┐╬│╠═╞╝÷úí | │⌡╚² | │⌡╚²├Γ╖╤┐╬│╠═╞╝÷úí |
┐╞─┐ú║│⌡╓╨╩²╤º └┤╘┤ú║ ╠Γ╨═ú║
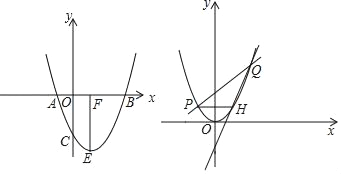
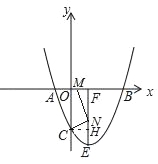
í╛╠Γ─┐í┐╥╤╓¬ú║╚τ═╝ú¼╖┤▒╚└²║»╩²y= ![]() ╡─═╝╧≤╙δ╥╗┤╬║»╩²y=x+b╡─═╝╧≤╜╗
╡─═╝╧≤╙δ╥╗┤╬║»╩²y=x+b╡─═╝╧≤╜╗
╙┌╡πAú¿1ú¼4ú⌐íó╡πBú¿-4ú¼nú⌐ú«

ú¿1ú⌐╟≤╥╗┤╬║»╩²║═╖┤▒╚└²║»╩²╡─╜Γ╬÷╩╜ú╗
ú¿2ú⌐╟≤í≈OAB╡─├µ╗²ú╗
ú¿3ú⌐╓▒╜╙╨┤│÷╥╗┤╬║»╩²╓╡┤≤╙┌╖┤▒╚└²║»╩²╓╡╡─╫╘▒Σ┴┐x╡─╚í╓╡╖╢╬ºú«
▓Θ┐┤┤≡░╕║═╜Γ╬÷>>
┐╞─┐ú║│⌡╓╨╩²╤º └┤╘┤ú║ ╠Γ╨═ú║
í╛╠Γ─┐í┐╬╩╠Γ╖ó╧╓ú║
ú¿![]() ú⌐╚τ═╝ó┘ú¼
ú⌐╚τ═╝ó┘ú¼![]() ╓╨ú¼
╓╨ú¼![]() ú¼
ú¼![]() ú¼
ú¼![]() ú¼╡π
ú¼╡π![]() ╩╟
╩╟![]() ▒▀╔╧╚╬╥Γ╥╗╡πú¼╘≥
▒▀╔╧╚╬╥Γ╥╗╡πú¼╘≥![]() ╡─╫ε╨í╓╡╬¬__________ú«
╡─╫ε╨í╓╡╬¬__________ú«
ú¿![]() ú⌐╚τ═╝ó┌ú¼╛╪╨╬
ú⌐╚τ═╝ó┌ú¼╛╪╨╬![]() ╓╨ú¼
╓╨ú¼![]() ú¼
ú¼![]() ú¼╡π
ú¼╡π![]() íó╡π
íó╡π![]() ╖╓▒≡╘┌
╖╓▒≡╘┌![]() íó
íó![]() ╔╧ú¼╟≤
╔╧ú¼╟≤![]() ╡─╫ε╨í╓╡ú«
╡─╫ε╨í╓╡ú«
ú¿![]() ú⌐╚τ═╝ó█ú¼╛╪╨╬
ú⌐╚τ═╝ó█ú¼╛╪╨╬![]() ╓╨ú¼
╓╨ú¼![]() ú¼
ú¼![]() ú¼╡π
ú¼╡π![]() ╩╟
╩╟![]() ▒▀╔╧╥╗╡πú¼╟╥
▒▀╔╧╥╗╡πú¼╟╥![]() ú¼╡π
ú¼╡π![]() ╩╟
╩╟![]() ▒▀╔╧╡─╚╬╥Γ╥╗╡πú¼░╤
▒▀╔╧╡─╚╬╥Γ╥╗╡πú¼░╤![]() ╤╪
╤╪![]() ╖¡╒█ú¼╡π
╖¡╒█ú¼╡π![]() ╡─╢╘╙ª╡π╬¬╡π
╡─╢╘╙ª╡π╬¬╡π![]() ú¼┴¼╜╙
ú¼┴¼╜╙![]() íó
íó![]() ú¼╦─▒▀╨╬
ú¼╦─▒▀╨╬![]() ╡─├µ╗²╩╟╖±┤µ╘┌╫ε╨í╓╡ú¼╚⌠┤µ╘┌ú¼╟≤╒Γ╕÷╫ε╨í╓╡╝░┤╦╩▒
╡─├µ╗²╩╟╖±┤µ╘┌╫ε╨í╓╡ú¼╚⌠┤µ╘┌ú¼╟≤╒Γ╕÷╫ε╨í╓╡╝░┤╦╩▒![]() ╡─│ñ╢╚ú╗╚⌠▓╗┤µ╘┌ú¼╟δ╦╡├≈└φ╙╔ú«
╡─│ñ╢╚ú╗╚⌠▓╗┤µ╘┌ú¼╟δ╦╡├≈└φ╙╔ú«
▓Θ┐┤┤≡░╕║═╜Γ╬÷>>
┐╞─┐ú║│⌡╓╨╩²╤º └┤╘┤ú║ ╠Γ╨═ú║
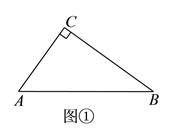
í╛╠Γ─┐í┐╚τ═╝ú¼╘┌╞╜├µ╓▒╜╟╫°▒Ω╧╡╓╨╙╨╥╗╓▒╜╟╚²╜╟╨╬AOBú¼O╬¬╫°▒Ω╘¡╡πú¼OAú╜1ú¼taní╧BAOú╜3ú¼╜½┤╦╚²╜╟╨╬╚╞╘¡╡πO─µ╩▒╒δ╨²╫¬90íπú¼╡├╡╜í≈DOCú¼┼╫╬∩╧▀yú╜ax2+bx+c╛¡╣²╡πAíóBíóCú«
(1)╟≤┼╫╬∩╧▀╡─╜Γ╬÷╩╜ú╗
(2)╚⌠╡πP╩╟╡┌╢■╧≤╧▐─┌┼╫╬∩╧▀╔╧╡─╢»╡πú¼╞Σ║ß╫°▒Ω╬¬tú¼╔Φ┼╫╬∩╧▀╢╘│╞╓ßl╙δx╓ß╜╗╙┌╥╗╡πEú¼┴¼╜╙PEú¼╜╗CD╙┌Fú¼╟≤╥╘CíóEíóF╬¬╢Ñ╡π╚²╜╟╨╬╙δí≈COD╧α╦╞╩▒╡πP╡─╫°▒Ωú«

▓Θ┐┤┤≡░╕║═╜Γ╬÷>>
┐╞─┐ú║│⌡╓╨╩²╤º └┤╘┤ú║ ╠Γ╨═ú║
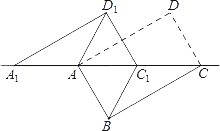
í╛╠Γ─┐í┐╚τ═╝ú¼╜½╛╪╨╬ABCD╤╪╢╘╜╟╧▀AC╝⌠┐¬ú¼╘┘░╤í≈ACD╤╪CA╖╜╧≥╞╜╥╞╡├╡╜í≈A1C1D1ú¼┴¼╜ßAD1ú¼BC1ú«╚⌠í╧ACBú╜30íπú¼ABú╜1ú¼CC1ú╜xú¼í≈ACD╙δí≈A1C1D1╓╪╡■▓┐╖╓╡─├µ╗²╬¬sú¼╘≥╧┬┴╨╜ß┬█ú║ó┘í≈A1AD1í╒í≈CC1Bó┌╡▒xú╜1╩▒ú¼╦─▒▀╨╬ABC1D1╩╟┴Γ╨╬ ó█╡▒xú╜2╩▒ú¼í≈BDD1╬¬╡╚▒▀╚²╜╟╨╬ ó▄sú╜![]() ú¿x⌐ü2ú⌐2ú¿0ú╝xú╝2ú⌐ú¼╞Σ╓╨╒²╚╖╡─╙╨ú¿ííííú⌐
ú¿x⌐ü2ú⌐2ú¿0ú╝xú╝2ú⌐ú¼╞Σ╓╨╒²╚╖╡─╙╨ú¿ííííú⌐
A. 1 ╕÷B. 2 ╕÷C. 3 ╕÷D. 4 ╕÷
▓Θ┐┤┤≡░╕║═╜Γ╬÷>>
┐╞─┐ú║│⌡╓╨╩²╤º └┤╘┤ú║ ╠Γ╨═ú║
í╛╠Γ─┐í┐─│┼⌐╗º│╨░ⁿ╗─╔╜╓╓╓▓─│▓·╞╖╓╓├█Φ╓![]() ╥╤╓¬╕├├█Φ╓╡─│╔▒╛╝█╬¬8╘¬
╥╤╓¬╕├├█Φ╓╡─│╔▒╛╝█╬¬8╘¬![]() ╟º┐╦ú¼═╢╚δ╩╨│í╧·╩█╩▒ú¼╡≈▓Θ╩╨│í╨╨╟Θú¼╖ó╧╓╕├├█Φ╓╧·╩█▓╗╗ß┐≈▒╛ú¼╟╥├┐╠∞╧·┴┐
╟º┐╦ú¼═╢╚δ╩╨│í╧·╩█╩▒ú¼╡≈▓Θ╩╨│í╨╨╟Θú¼╖ó╧╓╕├├█Φ╓╧·╩█▓╗╗ß┐≈▒╛ú¼╟╥├┐╠∞╧·┴┐![]() ╟º┐╦
╟º┐╦![]() ╙δ╧·╩█╡Ñ╝█
╙δ╧·╩█╡Ñ╝█![]() ╘¬
╘¬![]() ╟º┐╦
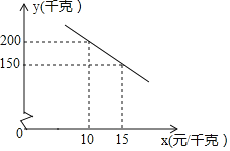
╟º┐╦![]() ╓«╝Σ╡─║»╩²╣╪╧╡╚τ═╝╦∙╩╛ú«
╓«╝Σ╡─║»╩²╣╪╧╡╚τ═╝╦∙╩╛ú«
![]() ╟≤y╙δx╡─║»╩²╣╪╧╡╩╜ú¼▓ó╨┤│÷x╡─╚í╓╡╖╢╬ºú╗
╟≤y╙δx╡─║»╩²╣╪╧╡╩╜ú¼▓ó╨┤│÷x╡─╚í╓╡╖╢╬ºú╗
![]() ╡▒╕├╞╖╓╓├█Φ╓╢¿╝█╬¬╢α╔┘╩▒ú¼├┐╠∞╧·╩█╗±╡├╡─└√╚≤╫ε┤≤ú┐╫ε┤≤└√╚≤╩╟╢α╔┘ú┐
╡▒╕├╞╖╓╓├█Φ╓╢¿╝█╬¬╢α╔┘╩▒ú¼├┐╠∞╧·╩█╗±╡├╡─└√╚≤╫ε┤≤ú┐╫ε┤≤└√╚≤╩╟╢α╔┘ú┐
▓Θ┐┤┤≡░╕║═╜Γ╬÷>>
┐╞─┐ú║│⌡╓╨╩²╤º └┤╘┤ú║ ╠Γ╨═ú║
í╛╠Γ─┐í┐╘┌╚ñ╬╢╘╦╢»╗ßí░╢¿╡π═╢└║í▒╧ε─┐╓╨ú¼╬╥╨ú╞▀─Ω╝╢░╦╕÷░α╡─═╢└║│╔╝¿![]() ╡Ñ╬╗ú║╕÷
╡Ñ╬╗ú║╕÷![]() ╖╓▒≡╬¬ú║24ú¼20ú¼19ú¼20ú¼22ú¼23ú¼20ú¼
╖╓▒≡╬¬ú║24ú¼20ú¼19ú¼20ú¼22ú¼23ú¼20ú¼![]() ╘≥╒Γ╫Θ╩²╛▌╓╨╡─╓┌╩²║═╓╨╬╗╩²╖╓▒≡╩╟
╘≥╒Γ╫Θ╩²╛▌╓╨╡─╓┌╩²║═╓╨╬╗╩²╖╓▒≡╩╟![]() íííí
íííí![]()
A. 22╕÷íó20╕÷ B. 22╕÷íó21╕÷ C. 20╕÷íó21╕÷ D. 20╕÷íó22╕÷
▓Θ┐┤┤≡░╕║═╜Γ╬÷>>
┐╞─┐ú║│⌡╓╨╩²╤º └┤╘┤ú║ ╠Γ╨═ú║
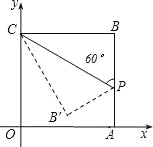
í╛╠Γ─┐í┐╚τ═╝ú¼╘┌╞╜├µ╓▒╜╟╫°▒Ω╧╡╓╨ú¼OABC╩╟╒²╖╜╨╬ú¼╡πA╡─╫°▒Ω╩╟ú¿4ú¼0ú⌐ú¼╡πP╬¬▒▀AB╔╧╥╗╡πú¼í╧CPBú╜60íπú¼╤╪CP╒█╡■╒²╖╜╨╬ú¼╒█╡■║≤ú¼╡πB┬Σ╘┌╞╜├µ─┌╡πBíΣ┤ªú¼╘≥BíΣ╡π╡─╫°▒Ω╬¬ú¿ííííú⌐
A. ú¿2ú¼2![]() ú⌐B. ú¿
ú⌐B. ú¿![]() ú¼
ú¼![]() ú⌐C. ú¿2ú¼
ú⌐C. ú¿2ú¼![]() ú⌐D. ú¿
ú⌐D. ú¿![]() ú¼
ú¼![]() ú⌐
ú⌐
▓Θ┐┤┤≡░╕║═╜Γ╬÷>>
┐╞─┐ú║│⌡╓╨╩²╤º └┤╘┤ú║ ╠Γ╨═ú║
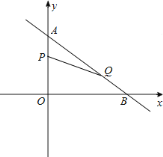
í╛╠Γ─┐í┐╚τ═╝ú¼╘┌╞╜├µ╓▒╜╟╫°▒Ω╧╡╓╨ú¼╥╤╓¬Rtí≈AOB╡─┴╜╠⌡╓▒╜╟▒▀OAíóOB╖╓▒≡╘┌y╓ß║═x╓ß╔╧ú¼▓ó╟╥OAíóOB╡─│ñ╖╓▒≡╩╟╖╜│╠x2ú¡7xú½12=0╡─┴╜╕∙ú¿OAú╝OBú⌐ú¼╢»╡πP┤╙╡πA┐¬╩╝╘┌╧▀╢╬AO╔╧╥╘├┐├δ1╕÷╡Ñ╬╗│ñ╢╚╡─╦┘╢╚╧≥╡πO╘╦╢»ú╗═¼╩▒ú¼╢»╡πQ┤╙╡πB┐¬╩╝╘┌╧▀╢╬BA╔╧╥╘├┐├δ2╕÷╡Ñ╬╗│ñ╢╚╡─╦┘╢╚╧≥╡πA╘╦╢»ú¼╔Φ╡πPíóQ╘╦╢»╡─╩▒╝Σ╬¬t├δ.
ú¿1ú⌐╟≤AíóB┴╜╡π╡─╫°▒Ω.
ú¿2ú⌐╟≤╡▒t╬¬║╬╓╡╩▒ú¼í≈APQ╙δí≈AOB╧α╦╞?
▓Θ┐┤┤≡░╕║═╜Γ╬÷>>
░┘╢╚╓┬╨┼ - ┴╖╧░▓ß┴╨▒φ - ╩╘╠Γ┴╨▒φ
║■▒▒╩í╗Ñ┴¬═°╬Ñ╖¿║═▓╗┴╝╨┼╧ó╛┘▒¿╞╜╠¿ | ═°╔╧╙╨║ª╨┼╧ó╛┘▒¿╫¿╟° | ╡τ╨┼╒⌐╞¡╛┘▒¿╫¿╟° | ╔µ└·╩╖╨Θ╬▐╓≈╥σ╙╨║ª╨┼╧ó╛┘▒¿╫¿╟° | ╔µ╞≤╟╓╚¿╛┘▒¿╫¿╟°
╬Ñ╖¿║═▓╗┴╝╨┼╧ó╛┘▒¿╡τ╗░ú║027-86699610 ╛┘▒¿╙╩╧Σú║58377363@163.com