练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    用科学计数法表示的数-3.6×10-4写成小数是（ ）

    A. 0.00036 B. -0.0036 C. -0.00036 D. -36000

    C 【解析】试题解析：-3.6×10-4写成小数是 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图，△ABC中，AB=AC，作AD⊥BC，CE⊥AB，垂足分别为D，E，AD和CE相交于点F，若已知AE=CE.

    (1)求证：△AEF≌△CEB；

    (2)求证：AF=2CD

    （1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）要证明△AEF≌△CEB，已知条件有AE=EC，∠AEF=∠BEC=90°，还差一个条件，由AD⊥BC，CE⊥AB可得∠B+∠BAD=90°，∠B+∠BCE=90°，所以得出∠EAF=∠ECB，因此可证明出△AEF≌△CEB；（2）由（1）结论可得：AF=BC，即要证明BC=2CD，由等腰三角形三线合一性质不难证明. 试题解...

    查看答案和解析>>

    科目：初中数学 来源：江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    已知无论n取什么实数，点P（n, 4n-3）都在直线l上，若Q（a， b）是直线l上的点，则4a-b的平方根等于（　　）

    A. B. 1 C. D.

    D 【解析】试题解析：∵令n=0，则P（0，-3）；再令n=1，则P（1，1），由于n不论为何值此点均在直线l上， ∴设此直线的解析式为y=kx+b（k≠0）， ∴， 解得， ∴此直线的解析式为：y=4x-3， ∵Q（a，b）是直线l上的点， ∴4a-3=b，即4a-b=3， ∴4a-b的平方根等于 故选D.

    查看答案和解析>>

    科目：初中数学 来源：湖南省武冈市2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    若关于x的不等式组的整数解共有3个，则a的取值范围为_______

    －2﹤x≤－1 【解析】试题解析：由原不等式得 其整数解必为1，0，?1， 故 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：湖南省武冈市2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    一艘轮船在静水中的最大航速为30千米/时，它沿江以最大航速顺流航行100千米所用时间，与以最大航速逆流航行60千米所用时间相等，江水的流速为多少？设江水的流速为千米/时，则可列方程（ ）

    A. 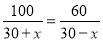B.

    C. D.

    A 【解析】设江水的流速为x千米/时， . 故选A.

    查看答案和解析>>

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    某服装厂生产一种夹克和T恤，夹克每件定价100元，T恤每件定价60元，厂方在开展促销活动期间，向客户提供两种优惠方案：①买一件夹克送一件T恤 ②夹克和T恤都按定价的8折付款．

    现某客户要到该服装厂购买夹克30件，T恤x件（x＞30）．

    （1）若按方案①购买夹克和T恤共需 元（用含x的式子表示），若按方案②购买夹克和T恤共需 元（用含x的式子表示）

    （2）若x=40，通过计算说明按方案①，②，哪种方案购买较为合算？

    （3）当购买多少件T恤时，按以上两种方案购买所付价钱一样多？

    （1） 60x+1200，48x+2400；（2）按方案①购买较合算；（3）当购买100件T恤时，按以上两种方案购买所付钱一样多． 【解析】试题分析：（1）该客户按方案①购买，夹克需付款30×100=3000；T恤需付款，若该客户按方案②购买，夹克需付款30×100×80%=2400；T恤需付款 （2）把分别代入（1）中的代数式中，再求和得到按方案①购买所需费用=30×100+60（40-...

    查看答案和解析>>

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    用同样大小的黑色棋子按如图所示的规律摆放：

    则第5个图案有____个棋子，第n个图案有____个棋子．（用含n的式子表示）

    18 3n+3． 【解析】试题解析：∵第1个图形有6个棋子， 第2个图形有6+3=9个棋子， 第3个图形有6+3×2=12个棋子， 第4个图形有6+3×4=18个棋子， ∴第5个图形有18个棋子， ∴第n个图形有棋子(3n+3)个[或6+3(n?1)等]. 故答案为：18，3n+3.

    查看答案和解析>>

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    -5的倒数是（ ）

    A. 5 B. -5 C. D.

    D 【解析】试题解析： 的倒数是 故选D.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：填空题

    如图，OA⊥OB，∠BOC=300，OD平分∠AOC，则∠BOD= _____．

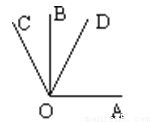
    30° 【解析】∵OA⊥OB，∴∠AOB=90°， ∵∠BOC=30°，∴∠AOC=∠AOB+∠BOC=120°， ∵OD平分∠AOC，∴∠AOD=∠AOC=60°， ∴∠BOD=∠AOB-∠AOD=30°， 故答案为：30°.

    查看答案和解析>>

    同步练习册答案