
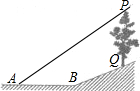
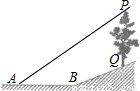
 已知:如图,在坡度为i=1:2.4的斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A、B、P、Q在同一平面上,PQ⊥AB.求:香樟树PQ的高度.
已知:如图,在坡度为i=1:2.4的斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A、B、P、Q在同一平面上,PQ⊥AB.求:香樟树PQ的高度.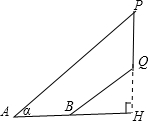
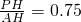 .
.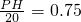 ,
,

科目:初中数学 来源: 题型:
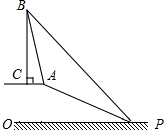 22.已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:
22.已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•金华模拟)已知:如图,在坡度为i=1:2.4的斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A、B、P、Q在同一平面上,PQ⊥AB.求:香樟树PQ的高度.
(2013•金华模拟)已知:如图,在坡度为i=1:2.4的斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A、B、P、Q在同一平面上,PQ⊥AB.求:香樟树PQ的高度.查看答案和解析>>
科目:初中数学 来源: 题型:
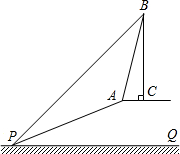 (2013•瑶海区一模)已知:如图,在大蜀山山顶有一斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座安徽卫视发射塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°,求:
(2013•瑶海区一模)已知:如图,在大蜀山山顶有一斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座安徽卫视发射塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°,求:查看答案和解析>>
科目:初中数学 来源:2012年上海市闸北区中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com