
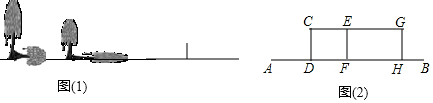
分析 A.(1)利用中心投影的定义画图;
(2)过点O作射线OB,交地面于点B;
B.(1)利用中心投影的定义画图;
(2)设小明原来的速度为xm/s,则CE=2xm,AM=AF-MF=(4x-1.2)m,EG=2×1.5x=3xm,BM=AB-AM=12-(4x-1.2)=13.2-4x,根据相似三角形的判定方法得到△OCE∽△OAM,△OEG∽△OMB,则$\frac{CE}{AM}=\frac{OE}{OM}$,$\frac{EG}{BM}$=$\frac{OE}{OM}$,$\frac{EG}{BM}$,即$\frac{2x}{4x-1.2}$=$\frac{3x}{13.2-4x}$,然后解方程解决.
解答 解:从A,B两题中任选一题解答,我选择A,
A.(1)如图1,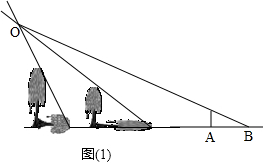
(2)如图所示,线段AB即为所求线段;
故答案为:A.
B.(1)如图2,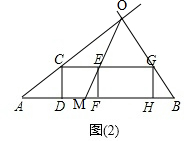
(2)设小明原来的速度为xm/s,则CE=2xm,AM=AF-MF=(4x-1.2)m,EG=2×1.5x=3xm,BM=AB-AM=12-(4x-1.2)=13.2-4x,
∵点C,E,G在一条直线上,CG∥AB,
∴△OCE∽△OAM,△OEG∽△OMB,
∴$\frac{CE}{AM}=\frac{OE}{OM}$,$\frac{EG}{BM}$=$\frac{OE}{OM}$,
∴$\frac{CE}{AM}$=$\frac{EG}{BM}$,即$\frac{2x}{4x-1.2}$=$\frac{3x}{13.2-4x}$,
解得x=1.5,
经检验x=1.5为方程的解,
∴小明原来的速度为1.5m/s,
故答案为:1.5m/s.
点评 本题考查了相似三角形的应用:从实际问题中抽象出几何图形,然后利用相似比计算相应线段的长.也考查了中心投影.


科目:初中数学 来源: 题型:解答题
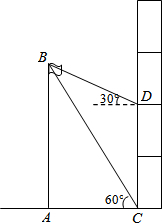 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼五楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知CD=12米,求旗杆AB的高度.
某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼五楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知CD=12米,求旗杆AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
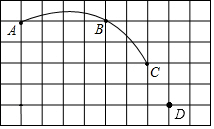 阅读下面的材料,回答问题:
阅读下面的材料,回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
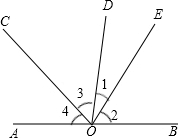 如图,已知O为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE,且OC平分∠AOD,∠BOE=3∠DOE,∠COE=70°.
如图,已知O为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE,且OC平分∠AOD,∠BOE=3∠DOE,∠COE=70°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com