
【题目】如图,已知AD是△ABC的角平分线,AD的中垂线交AB于点F,交BC的延长线于点E.以下四个结论:(1)∠EAD=∠EDA;(2)DF∥AC;(3)∠FDE=90°;(4)∠B=∠CAE.恒成立的结论有( )

A. (1)(2)B. (2)(3)(4)C. (1)(2)(4)D. (1)(2)(3)(4)
【答案】C
【解析】
由中垂线的性质知,DE=AE,由等边对等角知,∠EAD=∠EDA,故可判断(1)
由中垂线的性质知,FD=FA∠FDA=∠FAD,由AD平分∠BAC∠FAD=∠DAC,∠FDA=∠DACDF∥AC,故可判断(2)
由三角形的外角与内角的关系知,∠EAD=∠DAC+∠CAE,∠EDA=∠B+∠BAD,而∠EAD=∠EDA,∠FAD=∠DAC,故有∠EAC=∠B.故可判断(4)
(1)∵EF是AD的中垂线,
∴DE=AE.
∴∠EAD=∠EDA.故(1)正确
∵EF为中垂线,
∴FD=FA.
∴∠FDA=∠FAD.
∵AD平分∠BAC,
∴∠FAD=∠DAC,
所以∠FDA=∠DAC.
∴DF∥AC.故(2)正确
∵∠EAD=∠EDA,∠EAD=∠DAC+∠CAE,∠EDA=∠B+∠BAD,
∴∠DAC+∠CAE=∠B+∠BAD,
∵∠FAD=∠DAC,
∴∠EAC=∠B.故(4)正确
故选:C


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
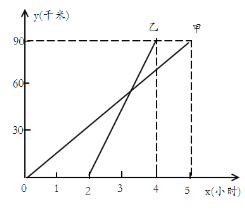
【题目】如图表示甲骑摩托车和乙驾驶汽车沿相同的路线行驶90千米,由A地到B地时,行驶的路程y(千米)与经过的时间x(小时)之间的关系。请根据图象填空:
(1)摩托车的速度为_____千米/小时;汽车的速度为_____千米/小时;
(2)汽车比摩托车早_____小时到达B地。
(3)在汽车出发后几小时,汽车和摩托车相遇?说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上

(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=2,AC=2![]() ,点F是AD的中点,直接写出CF的长是 .
,点F是AD的中点,直接写出CF的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乌鲁木齐周边多地盛产草莓,今年某水果销售店在草莓销售旺季,以15元/kg 的成本价进50kg有机草莓,销售人员销售发现草莓损坏率为25%;
(1)对于水果店来说完好的草莓实际成本价是多少元/kg?
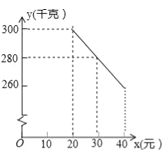
(2)按照这个实际成本设计销售单价,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象,设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的图角如图3,则下列结论:①abc>0;②a+b+c=2;③a>![]() ;④b<1.其中正确的结论是( )
;④b<1.其中正确的结论是( )

A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.

证明:∵∠4=∠AFD( ),
∵∠3=∠4(已知),
∴∠3=∠ ( ).
∵∠1=∠2(已知),
∴∠1+∠3=∠2+∠AFD( ).
∴∠D=∠ ( ).
∴∠B=∠ ( ).
∴∠________=∠ ( ).
∴AD∥BE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为160元,200元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入/元 | |
A种型号/台 | B种型号/台 | ||
第1周 | 3 | 5 | 1800 |
第2周 | 4 | 10 | 3200 |
(1)A、B两种型号的电风扇的销售单价是多少?
(2)若该超市准备用不多于5400元的金额再次采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com