
【题目】如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).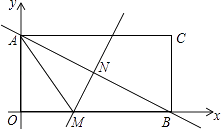
(1)求对角线AB所在直线的函数关系式;
(2)对角线AB的垂直平分线MN交x轴于点M,连接AM,求线段AM的长;
(3)若点P是直线AB上的一个动点,当△PAM的面积与长方形OABC的面积相等时,求点P的坐标.
【答案】
(1)
解:∵四边形AOBC为长方形,且点C的坐标是(8,4),
∴AO=CB=4,OB=AC=8,
∴A点坐标为(0,4),B点坐标为(8,0).
设对角线AB所在直线的函数关系式为y=kx+b,
则有 ![]() ,解得:
,解得:  ,
,
∴对角线AB所在直线的函数关系式为y=﹣ ![]() x+4
x+4
(2)
解:∵四边形AOBC为长方形,且MN⊥AB,
∴∠AOB=∠MNB=90°,
又∵∠ABO=∠MBN,
∴△AOB∽△MNB,
∴ ![]() .
.
∵AO=CB=4,OB=AC=8,
∴由勾股定理得:AB= ![]() =4
=4 ![]() ,
,
∵MN垂直平分AB,
∴BN=AN= ![]() AB=2
AB=2 ![]() .
.
![]() =
= ![]() =
= ![]() ,即MB=5.
,即MB=5.
OM=OB﹣MB=8﹣5=3,
由勾股定理可得:
AM= ![]() =5
=5
(3)
解:∵OM=3,
∴点M坐标为(3,0).
又∵点A坐标为(0,4),
∴直线AM的解析式为y=﹣ ![]() x+4.
x+4.
∵点P在直线AB:y=﹣ ![]() x+4上,
x+4上,
∴设P点坐标为(m,﹣ ![]() m+4),
m+4),
点P到直线AM: ![]() x+y﹣4=0的距离h=
x+y﹣4=0的距离h= 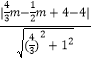 =
= ![]() .
.
△PAM的面积S△PAM= ![]() AMh=
AMh= ![]() |m|=SOABC=AOOB=32,
|m|=SOABC=AOOB=32,
解得m=± ![]() ,
,
故点P的坐标为( ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() )
)
【解析】(1)由坐标系中点的意义结合图形可得出A、B点的坐标,设出对角线AB所在直线的函数关系式,由待定系数法即可求得结论;(2)由相似三角形的性质找到BM的长度,再结合OM=OB﹣BM得出OM的长,根据勾股定理即可得出线段AM的长;(3)先求出直线AM的解析式,设出P点坐标,由点到直线的距离求出AM边上的高h,再结合三角形面积公式与长方形面积公式即可求出P点坐标.
【考点精析】解答此题的关键在于理解一次函数的图象和性质的相关知识,掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
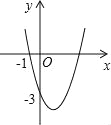
A. ﹣3<P<﹣1 B. ﹣6<P<0 C. ﹣3<P<0 D. ﹣6<P<﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
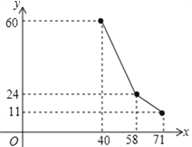
【题目】国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.
(1)求日销售y(件)与销售价x (元/件)之间的函数关系式;
(2)若暂不考虑还贷,当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;
(3)若该店只有2名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列说法:①棱柱的上、下底面的形状相同;②相等的角是对顶角;③若AB=BC,则点B为线段AC的中点;④直线外一点与直线上各点连接的所有线段中,垂线段最短.
其中正确说法的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
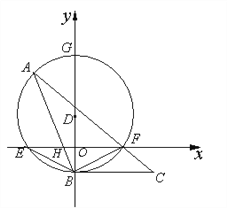
【题目】如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在![]() 上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
(1)判断直线BC与⊙D的位置关系,并说明理由;
(2)求证:BE2=BH·AB;
(3) 若点E坐标为(-4,0),点B的坐标为(0,-2),AB=8,求F与A两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,已知点A(0,2)、点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
(1)填空:点D的坐标为_________,点E的坐标为_______________.
(2)若抛物线![]() 经过A、D、E三点,求该抛物线的解析式.
经过A、D、E三点,求该抛物线的解析式.
(3)若正方形和抛物线均以每秒![]() 个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在
个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在![]() 轴上时,正方形和抛物线均停止运动.
轴上时,正方形和抛物线均停止运动.
①在运动过程中,设正方形落在y轴右侧部分的面积为![]() ,求
,求![]() 关于平移时间
关于平移时间![]() (秒)的函数关系式,并写出相应自变量
(秒)的函数关系式,并写出相应自变量![]() 的取值范围.
的取值范围.
②运动停止时,求抛物线的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角三角形ABC中,直线L为BC的中垂线,射线BM为∠ABC的角平分线,L与M相交于P点,若∠A=60°,∠ACP=24°,则∠ABP的度数为 . 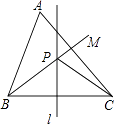
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com