
【题目】完成下列证明过程.
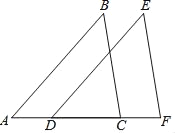
如图,已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.
证明:∵AB∥DE
∴∠_____=∠_____(_______)
∵AD=CF
∴AD+DC=CF+DC即_____
在△ABC和△DEF中AB=DE_____
∴△ABC≌△DEF_____.
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.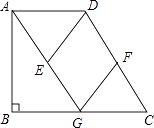
(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是 ![]() .
.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形纸片ABC中,AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交于点P1;设P1D的中点为D1 , 第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2 , 第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;…;设Pn﹣1Dn﹣2的中点为Dn﹣1 , 第n次将纸片折叠,使点A与点Dn﹣1重合,折痕与AD交于点Pn(n>2),则AP6的长为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,连接DE,CF交AD于G,点E是BF中点.
(1)求证:△AFG∽△AED
(2)若FG=2,G为AD中点,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座城市的中心火车站A,B两站相距360 km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54 km/h,当动车到达B站时,特快列车恰好到达距离A站135 km处的C站.求动车和特快列车的平均速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中国足球改革总体方案》提出足球要进校园,为了解某校学生对校园足球喜爱的情况,随机对该校部分学生进行了调查,将调查结果分为“很喜欢”、“较喜欢”、“一般”、“不喜欢”四个等级,并根据调查结果绘制成了如下两幅不完整的统计图;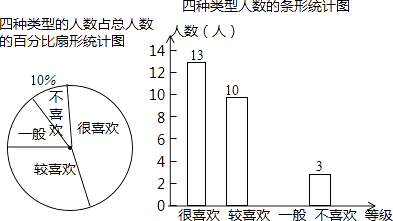
(1)一共调查了名学生,请补全条形统计图;
(2)在此次调查活动中,选择“一般”的学生中只有两人来自初三年级,现在要从选择“一般”的同学中随机抽取两人来谈谈各自对校园足球的感想,请用画树状图或列表法求选中的两人刚好都来自初三年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(6x4﹣4x3+2x2)÷(﹣2x2)+3x2
(2)(x﹣5)(2x+5)+2x(3﹣x)
(3)(﹣1)2016+(﹣![]() )﹣2﹣(3.14﹣π)0
)﹣2﹣(3.14﹣π)0
(4)运用乘法公式计算:1122﹣113×111
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com