
【题目】已知锐角△ABC中,边BC长为12,高AD长为8
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K
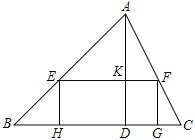
①求![]() 的值
的值
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值
(2)若ABAC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点时停止运动.点P也同时停止.点P,Q运动速度均为每秒1个单位长度,连接PQ,设运动时间为t(t>0)秒.
(1)当点Q从B点向A点运动时(未到达A点),
①当t=_____时PQ∥BC
②求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(2)伴随着P,Q两点的运动,线段PQ的垂直平分线为l:
①当l经过点A时,射线QP交AD于点E,求此时的t的值和AE的长;
②当l经过点B时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在钝角△ABC中,AB=5 cm,AC=10 cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1 cm/秒,点E运动的速度为2 cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
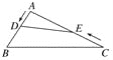
A. 2.5秒
B. 4.5秒
C. 2.5秒或4.5秒
D. 2.5秒或4秒
查看答案和解析>>
科目:初中数学 来源: 题型:
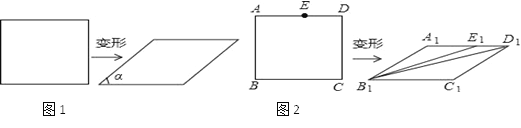
【题目】阅读理解:
我们知道,四边形具有不稳定性,容易变形,如图1,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把![]() 的值叫做这个平行四边形的变形度.
的值叫做这个平行四边形的变形度.
(1)若矩形发生变形后的平行四边形有一个内角是120度,则这个平行四边形的变形是 .
猜想证明:
(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2, ![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:
(3)如图2,在矩形ABCD中,E是AD边上的一点,且AB2=AEAD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4![]() (m>0),平行四边形A1B1C1D1的面积为2
(m>0),平行四边形A1B1C1D1的面积为2![]() (m>0),试求∠A1E1B1+∠A1D1B1的度数.
(m>0),试求∠A1E1B1+∠A1D1B1的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
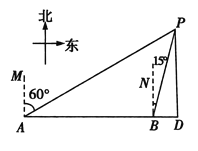
【题目】一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.
(1)求灯塔P到轮船航线的距离PD;(结果保留根号)
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每小时航行多少海里.(结果精确到1海里,参考数据![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)
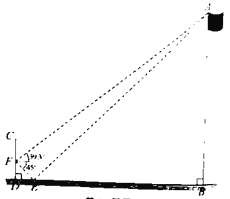
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为12,BC与BC边上的高AD之比为3:2,矩形EFGH的边EF在BC上,点H,G分别在边AB、AC上,且HG=2GF.
(1)求AD的长;
(2)求矩形EFGH的面积.
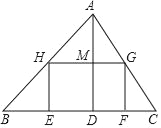
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2+bx+c的图象与x轴交于 A、B两点,与y轴交于点C,OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c的值;
(2)如图①,连接BE,线段OC上的点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;
(3)如图②,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.
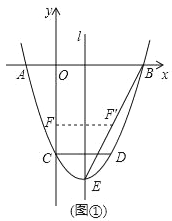

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,BC=4,以BC的中点O为圆心分别与AB,AC相切于D、E两点,则![]() 的长为( )
的长为( )
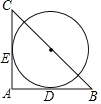
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() π
π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com