
【题目】已知![]() ,试探究并回答下列问题:
,试探究并回答下列问题:
(1)是否存在一点![]() ,使它到
,使它到![]() 两点的距离之和等于
两点的距离之和等于![]() ?并说明理由;
?并说明理由;
(2)是否存在一点![]() ,使它到
,使它到![]() 两点的距离之和等于
两点的距离之和等于![]() ?如果存在,那么它的位置是唯一的吗?
?如果存在,那么它的位置是唯一的吗?
(3)当点![]() 到
到![]() 两点的距离之和等于
两点的距离之和等于![]() 时,试说明点
时,试说明点![]() 的位置.
的位置.
【答案】(1)不存在,理由见解析;(2)存在,位置不唯一;(3)点C可以在线段AB的延长线上或反向延长线上或直线AB外.
【解析】
(1)根据两点之间线段最短进行判断;
(2)点C在线段AB上时,点C到A,B两点的距离之和等于6厘米;
(3)当点C在线段AB的延长线上或反向延长线上或直线AB外时,可满足点C到A,B两点的距离之和等于12厘米.
(1)不存在点C,使它到A,B两点的距离之和等于5厘米.因为两点之间线段最短;
(2)存在点C,使它到A,B两点的距离之和等于6厘米,此时点C在线段AB上,它的位置不唯一.
(3)当点C到A,B两点的距离之和等,12厘米时,点C可以在线段AB的延长线上或反向延长线上或直线AB外.


科目:初中数学 来源: 题型:
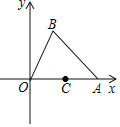
【题目】在平面直角坐标系中,点A、B、C的坐标分别为![]() ,
,![]() ,
,![]() ,点P,Q是
,点P,Q是![]() 边上的两个动点
边上的两个动点![]() 点P不与点C重合
点P不与点C重合![]() ,以P,O,Q为顶点的三角形与
,以P,O,Q为顶点的三角形与![]() 全等,则满足条件的点P的坐标为______.
全等,则满足条件的点P的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为非负实数,关于x的方程x2﹣(k+1)x+k=0和kx2﹣(k+2)x+k=0.
(1)试证:前一个方程必有两个非负实数根;
(2)当k取何值时,上述两个方程有一个相同的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
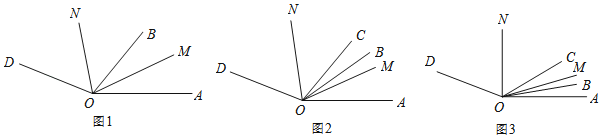
【题目】已知:∠AOD=150°,OB,OM,ON是∠AOD内的射线.
(1)如图1,若OM平分∠AOB,ON平分∠BOD.当射线OB绕点O在∠AOD内旋转时,
∠MON= °;
(2)OC也是∠AOD内的射线,如图2,若∠BOC=m°,OM平分∠AOC,ON平分∠BOD,
求∠MON的大小(用含m的式子表示);
(3)在(2)的条件下,若m=20,∠AOB=10°,当∠BOC在∠AOD内部绕O点以每秒2°的速度逆时针旋转t秒,如图3,若3∠AOM=2∠DON时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
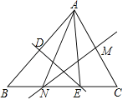
【题目】如图,△ABC中,∠BAC=80°,BC=12,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,NE=6,则∠NAE=______°,△EAN的周长=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,回答提出的问题.
我们知道:一个数![]() 的绝对值可以表示成
的绝对值可以表示成![]() ,它是一个非负数,在数轴上,
,它是一个非负数,在数轴上,![]() 表示
表示![]() 这个数在数轴上所对应的点到原点的距离(距离,当然不可能是负数),这正是绝对值的几何意义,比如说
这个数在数轴上所对应的点到原点的距离(距离,当然不可能是负数),这正是绝对值的几何意义,比如说![]() 表示2这个数在数轴上所对应的点到原点的距离,它是2,所以说
表示2这个数在数轴上所对应的点到原点的距离,它是2,所以说![]() 表示
表示![]() 这个数在数轴上所对应的点到原点的距离,它也是2,所以说
这个数在数轴上所对应的点到原点的距离,它也是2,所以说![]() ,严格来说,在数轴上,一个数
,严格来说,在数轴上,一个数![]() 在数轴上所对应的点到原点(原点对应的数为0)的距离应该表示为
在数轴上所对应的点到原点(原点对应的数为0)的距离应该表示为![]() ,但平时我们都写成
,但平时我们都写成![]() ,原因你明白.
,原因你明白.
(1)若给定![]() ,要找这样的x,请按照上面材料中的说法,解释它的几何意义并找出对应的
,要找这样的x,请按照上面材料中的说法,解释它的几何意义并找出对应的![]() ;
;
(2)实际上,对于数轴上任意两个数![]() 之间的距离我们也可以表示为
之间的距离我们也可以表示为![]() ,反过来,
,反过来,![]() 这个绝对值的几何意义就是:数轴上表示
这个绝对值的几何意义就是:数轴上表示![]() 与
与![]() 这两个数的点之间的距离,你能结合上面的叙述,解释
这两个数的点之间的距离,你能结合上面的叙述,解释![]() 的几何意义吗?请按你的理解说明:
的几何意义吗?请按你的理解说明:![]() 呢,如果能解释这个,你了不起;
呢,如果能解释这个,你了不起;
(3)若![]() ,请直接写出
,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC各顶点的坐标分别为A(-3,2),B(-4,-3),C(-1,-1),
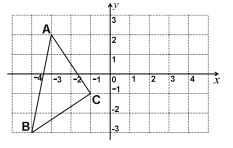
(1)请你画出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1的各点坐标;
(2)在y轴上找一点P,使△APC的周长最短。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
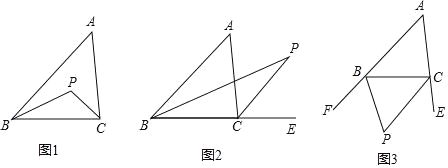
(1)如图1,在△ABC中,BP平分∠ABC,CP平分∠ACB.求证:∠P=90°+![]() ∠A.
∠A.
(2)如图2,在△ABC中,BP平分∠ABC,CP平分外角∠ACE.猜想∠P和∠A有何数量关系,并证明你的结论.
(3)如图3,BP平分∠CBF,CP平分∠BCE.猜想∠P和∠A有何数量关系,请直接写出结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com