
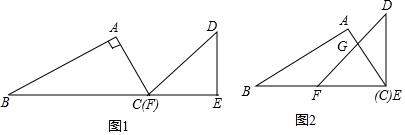
分析 (1)根据三角形的内角和得到∠ACB=60°,∠DFE=45°,于是得到结论;
(2)如图3,过G作GH⊥CF于H,解直角三角形即可得到结论;
(3)①当0<t≤2时,如图3,②当2<t≤$\sqrt{3}+$1时,如图4,③当$\sqrt{3}$+1<t≤3时,如图5,④当3<t≤4时,如图6,根据图形的面积的和差即可得到结论.
解答  解:(1)∵∠A=90°,∠B=30°,
解:(1)∵∠A=90°,∠B=30°,
∴∠ACB=60°,
∵∠DEF=90°,∠D=45°,
∴∠DFE=45°,
∴∠FGE=180°-∠ACB-∠GFE=75°;
故答案为:75°;
(2)如图3,过G作GH⊥CF于H,
∵∠GFH=45°,
∴FH=GH,
∵∠GCH=60°,
∴CH=$\sqrt{3}$GH,
∵CF=t,
∴GH+$\sqrt{3}$GH=t,
∴GH=$\frac{3-\sqrt{3}t}{2}$;
(3)①当0<t≤2时,如图3,S=$\frac{1}{2}$CF•GH=$\frac{1}{2}$×$\frac{(\sqrt{3}-1)t}{2}$×t=-$\frac{\sqrt{3}-1}{4}$t2;
②当2<t≤$\sqrt{3}+$1时,如图4,∵EF=DE=2,FH=GH=$\frac{(\sqrt{3}-1)t}{2}$,CF=t,
∴CE=t-2,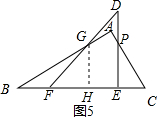
∴PE=$\sqrt{3}$(t-2),
∵HE=2-$\frac{(\sqrt{3}-1)t}{2}$,
∴S=S△GFH+S四边形PEHG=$\frac{1}{2}$($\frac{(\sqrt{3}-1)t}{2}$)2+$\frac{1}{2}$($\frac{(\sqrt{3}-1)t}{2}$+$\sqrt{3}$t-2$\sqrt{3}$)(2-$\frac{\sqrt{3}-1}{2}$t)=$\frac{\sqrt{3}-3}{4}$t2+($\sqrt{3}$-1)t-2$\sqrt{3}$;
③当$\sqrt{3}$+1<t≤3时,如图5,
∵∠A=90°,∠B=30°,AC=2cm,
∴BC=4cm,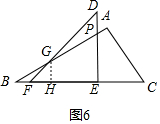
∴BF=4-t,CE=t-2,
∵GH=FH,BH=$\sqrt{3}$GH,
∴BH-FH=BF=4-t,
∴GH=$\frac{3-\sqrt{3}t}{2}$,
∴S=S△ABC-S△BGF-S△CPE=$\frac{1}{2}×$2×2$\sqrt{3}$-$\frac{1}{2}$(4-t)×$\frac{3-\sqrt{3}t}{2}$-$\frac{1}{2}$(t-2)•$\sqrt{3}$(t-2)=$\frac{3\sqrt{3}}{4}$t2-$\frac{3+4\sqrt{3}}{4}$t+2$\sqrt{3}$+3;
④当3<t≤4时,如图6,
由③得,GH=FH=$\frac{3-\sqrt{3}t}{2}$,CE=t-2,BF=4-t,
∴BE=4-CE=6-t,
∴PE=$\frac{6-t}{\sqrt{3}}$,
∴S=S△BPE-S△BFG=$\frac{1}{2}$(6-t)×$\frac{6-t}{\sqrt{3}}$-$\frac{1}{2}$×(4-t)×$\frac{3-\sqrt{3}t}{2}$=-$\frac{\sqrt{3}}{12}$t2+$\frac{6-7\sqrt{3}}{8}$t+6$\sqrt{3}$-3.
综上所述,S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}-1}{4}{t}^{2}(0<t≤2)}\\{\frac{\sqrt{3}-3}{4}{t}^{2}(\sqrt{3}-1)t-2\sqrt{3}(2<t≤\sqrt{3}+1)}\\{\frac{3\sqrt{3}}{4}{t}^{2}-\frac{3+4\sqrt{3}}{4}t+2\sqrt{3}+3(\sqrt{3}+1<t≤3)}\\{-\frac{\sqrt{3}}{12}{t}^{2}+\frac{6-7\sqrt{3}}{8}t+6\sqrt{3}-3(3<t≤4)}\end{array}\right.$.
点评 本题考查了直角三角形的性质,解直角三角形,根据图形的面积公式求函数的解析式,正确的作出图形是解题的关键.


科目:初中数学 来源: 题型:选择题
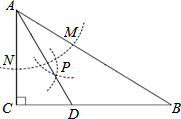 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列结论正确的有( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com