
分析 (1)根据图中的数据和平均数的计算方法可以解答本题;
(2)根据图中的数据和方差的计算方法可以解答本题;
(3)先判断,然后根据(2)中的结果和方差越小越稳定可以解答本题.
解答 解:(1)由题意可得,
$\overline{{x}_{甲}}=\frac{172+168+175+169+174+167+166+169}{8}$=170,
$\overline{{x}_{乙}}=\frac{164+175+174+165+162+173+172+175}{8}$=170,
答:甲、乙两名运动员跳高的平均成绩分别是170cm、170cm;
(2)由题意可得,
${{s}^{2}}_{甲}=\frac{(172-170)^{2}+(168-170)^{2}+(175-170)^{2}+(169-170)^{2}+(174-170)^{2}+(167-170)^{2}+(166-170)^{2}+(169-170)^{2}}{8}$=9.5,
s2乙=$\frac{(164-170)^{2}+(175-170)^{2}+(174-170)^{2}+(165-170)^{2}+(162-170)^{2}+(173-170)^{2}+(172-170)^{2}+(175-170)^{2}}{8}$=25.5;
(3)甲跳高运动员的成绩稳定,
理由:由(2)知,s2甲=9.5,s2乙=25.5,
∵9.5<25.5,
∴甲跳高运动员的成绩稳定.
点评 本题考查平均数、方差,解答本题的关键是明确平均数和方差的计算方法.


科目:初中数学 来源: 题型:填空题
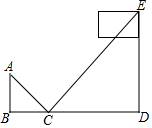 处看到旗杆顶部E,此时小军的站立点B与点C的水平距离为2m,旗杆底部D与点C的水平距离为12m.若小军的眼睛距离地面的高度为1.5m(即AB=1.5m),则旗杆的高度为9m.
处看到旗杆顶部E,此时小军的站立点B与点C的水平距离为2m,旗杆底部D与点C的水平距离为12m.若小军的眼睛距离地面的高度为1.5m(即AB=1.5m),则旗杆的高度为9m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
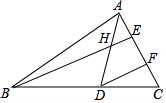 如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
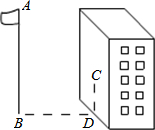 如图,某同学相测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.
如图,某同学相测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了乌龟所行的路程y1与出发所行的时间x的关系.
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了乌龟所行的路程y1与出发所行的时间x的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
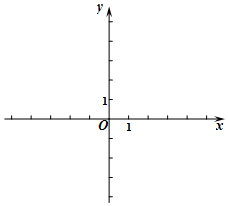 已知一次函数y=kx+b的图象经过点A(2,0),与y轴交于点B(0,4).
已知一次函数y=kx+b的图象经过点A(2,0),与y轴交于点B(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com