
【题目】某水果店经销一种高档水果,售价为每千克50元
(1)连续两次降价后售价为每千克32元,若每次下降的百分率相同.求平均下降的百分率;
(2)已知这种水果的进价为每千克40元,每天可售出500千克,经市场调查发现,若每千克涨价1元,日销售量将减少20千克,每千克应涨价多少元才能使每天获得的利润最大?
【答案】(1)20%(2)7.5元.
【解析】
(1)设每次降价的百分率为x,(1-x)2为两次降价的百分率,50降至32就是方程的平衡条件,列出方程求解即可;
(2)根据题意列出关于上涨价格m的二次函数关系式,根据二次函数的性质可得其最值情况.
(1)设每次下降的百分率为x,
根据题意得:50(1-x)2=32,
解得:x1=0.2,x2=1.8(不合题意舍去),
答:平均下降的百分率为20%.
(2)设每千克应涨价m元,每天的利润为W元,
W=(50-40+m)(500-20m)=-20m2+300m+5000,
则对称轴为m=-![]() =7.5,
=7.5,
∵a=-20<0,
∴当m=7.5时函数有最大值,
答:每千克应涨价7.5元才能使每天盈利最大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△OAB中,OA=AB,∠OAB=90°,点P从点O沿边OA、AB匀速运动到点B,过点P作PC⊥OB交OB于点C,线段AB=2![]() ,OC=x,S△POC=y,则能够反映y与x之间函数关系的图象大致是( )
,OC=x,S△POC=y,则能够反映y与x之间函数关系的图象大致是( )
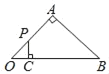
A. 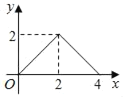 B.
B. 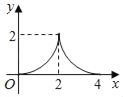
C. 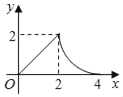 D.
D. 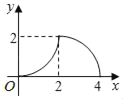
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,C、D为⊙O上的点,∠ACD=2∠A,CE⊥DB交DB的延长线于点E.
(1)求证:直线CE与⊙O相切;
(2)若AC=8,AB=10,求CE的长.
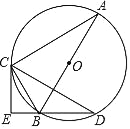
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠DAB=60°,AB=AD,线段BC绕点B顺时针旋转60°得到线段BE,连接AC、ED.
(1)求证:AC=DE;
(2)若DC=4,BC=6,∠DCB=30°,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为________.
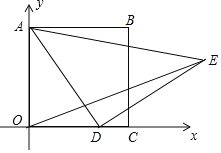
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为斜边作
为斜边作![]() ,使
,使![]() ,
,![]() 的面积记为
的面积记为![]() ,则
,则![]() ______;再以
______;再以![]() 为斜边作
为斜边作![]() ,使
,使![]() ,
,![]() 的面积记为
的面积记为![]() ,……,以此类推,则
,……,以此类推,则![]() ______.(用含
______.(用含![]() 的式子表示)
的式子表示)
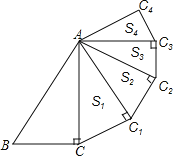
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com