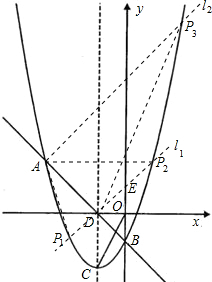
解:(1)∵直线y=kx-1经过A(-3,2),
∴把点A(-3,2)代入y=kx-1得:
2=-3k-1,∴k=-1,
把A(-3,2)、B(0,-1)、C(-1,-2)代入y=ax
2+bx+c
得
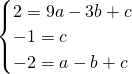
,
∴
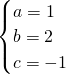
,
∴抛物线的解析式为y=x
2+2x-1.
(2)由
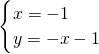
得D(-1,0),即点D在x轴上,
且|OD|=|OB|=1,
∴△BDO为等腰直角三角形,
∴∠BDO=45°,
①过点D作l
1⊥AB,交y轴于E,交抛物线于P
1、P
2两点,连接P
1A、P
2A,
则△P
1AD、△P
2AD都是满足条件的直角三角形,
∵∠EDO=90°-∠BDO=45°,
∴|OE|=|OD|=1,
∴点E(0,1),
∴直线l
1的解析式为y=x+1,
由
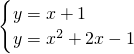
解得:
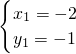
或
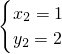
,
∴满足条件的点为P
1(-2,-1)、P
2(1,2);
②过点A作l
2⊥AB,交抛物线于另一点P
3,连接P
3D,则△P
3AD是满足条件的直角三角形,
∵l
1∥l
2且l
2过点A(-3,2)
∴l
2的解析式为y=x+5,
由
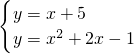
解得:
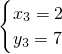
或

(舍去),
∴P
3的坐标为(2,7),
综上所述,满足条件的点为P
1(-2,-1)、P
2(1,2)、P
3(2,7).
(3)∵P
1(-2,-1),A(-3,2),D(-1,0),
∴P
1D=

,AD=2

;
而OC=1,CD=2,即P
1D:AD=OC:CD,
又∵∠OCD=∠P
1AD=90°,
∴△P
1AD∽△OCD,
同理可求得△P
2AD与△OCD不相似,△P
3AD与△OCD不相似;
故判断结果如下:
△P
1AD∽△OCD,
△P
2AD与△OCD不相似;
△P
3AD与△OCD不相似.
分析:(1)将点A的坐标代入直线AB的解析式中,即可确定k的值;根据A、B的坐标,可用待定系数法确定抛物线的解析式.
(2)根据抛物线的解析式,易求得D点坐标,可得OB=OD,即△OBD是等腰直角三角形;若△PAD是以AD为直角边的直角三角形,那么可分两种情况:
①以D为直角顶点,过D作直线l
1⊥AD,直线l
1与抛物线的交点即为所求的P点,设直线l
1与y轴的交点为E,由于△ODB是等腰直角三角形,故△ODE也是等腰直角三角形,即OD=OE,由此可得E点坐标,进而可根据D、E的坐标求出直线l
1的解析式,联立抛物线的解析式,即可得P点坐标;
②以A为直角顶点,过A作直线l
2⊥AD,同理直线l
2与抛物线的交点也符合P点的要求,由于直线l
1∥直线l
2,根据直线l
2的斜率和A点的坐标,即可求出直线l
2的解析式,然后联立抛物线的解析式,可得P点的坐标.
(3)根据C、D坐标,易得OC、CD的长,若(2)的直角三角形与△OCD相似,那么它们的直角边应该对应成比例,可先求出(2)中直角三角形的直角边长,然后再进行判断.
点评:此题考查了用待定系数法确定函数解析式的方法、直角三角形的判定、函数图象交点坐标的求法、相似三角形的判定和性质等知识,(2)题中,一定要根据直角三角形的不同直角顶点分类讨论,以免漏解.

 点,抛物线的顶点为C(-1,-2),对称轴交直线AB于点D,连接OC.
点,抛物线的顶点为C(-1,-2),对称轴交直线AB于点D,连接OC. 解:(1)∵直线y=kx-1经过A(-3,2),
解:(1)∵直线y=kx-1经过A(-3,2),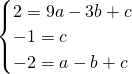 ,
,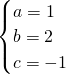 ,
,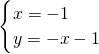 得D(-1,0),即点D在x轴上,
得D(-1,0),即点D在x轴上,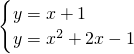
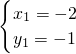 或
或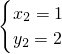 ,
,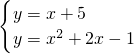
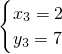 或
或 (舍去),
(舍去), ,AD=2
,AD=2 ;
;

 阅读快车系列答案
阅读快车系列答案 三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由. 平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式.
平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式. 如图所示:已知直线y=
如图所示:已知直线y=