
 24、如图,由4个全等的正方形组成“L”型图案,请你在图案中仅改变1个正方形的位置,使它变成轴对称图形,画出改变后的图形.
24、如图,由4个全等的正方形组成“L”型图案,请你在图案中仅改变1个正方形的位置,使它变成轴对称图形,画出改变后的图形. 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
 27、我们约定,若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A1是由△A复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1是由△A复制出△A1,又由△A1复制出△A2,再由△A2复制出△A3,形成了一个大三角形,记作△B.以下各题中的复制均是由△A开始的,由复制形成的多边形中的任意两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠.
27、我们约定,若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A1是由△A复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1是由△A复制出△A1,又由△A1复制出△A2,再由△A2复制出△A3,形成了一个大三角形,记作△B.以下各题中的复制均是由△A开始的,由复制形成的多边形中的任意两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 26、阅读:
26、阅读:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:黄冈难点课课练 八年级数学上册 题型:022
如图,正△ABC是由4个全等的正三角形构成的,则△ADE由△BDF绕________点旋转________得到.

查看答案和解析>>
科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第26期 总第182期 沪科版 题型:022
下图是上、下底面为全等的正六边形的礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两个全等的矩形.如果用彩色胶带如图包扎礼盒,所需胶带长度至少为
________cm(精确到0.1 cm).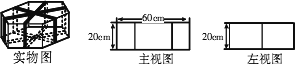
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com