
分析 (1)将分式拆项变形为[$\frac{a}{(a-b)(a-c)}$++$\frac{b}{(b-a)(b-c)}$+$\frac{c}{(c-a)(c-b)}$]+x[$\frac{a}{(a-b)(a-c)}$++$\frac{b}{(b-a)(b-c)}$+$\frac{c}{(c-a)(c-b)}$],依此即可求解;
(2)将等式左边变形为$\frac{{a}^{3}(b-c)-{b}^{3}(a-c)+{c}^{3}(a-b)}{(a-b)(a-c)(b-c)}$,再将分子因式分解为(b-c)(a-b)(a-c)(a+b+c),约分即可求解.
解答 解:(1)$\frac{a+x}{(a-b)(a-c)}$+$\frac{b+x}{(b-a)(b-c)}$+$\frac{c+x}{(c-a)(c-b)}$
=$\frac{a}{(a-b)(a-c)}$+$\frac{x}{(a-b)(a-c)}$+$\frac{b}{(b-a)(b-c)}$+$\frac{x}{(b-a)(b-c)}$+$\frac{c}{(c-a)(c-b)}$+$\frac{x}{(c-a)(c-b)}$
=[$\frac{a}{(a-b)(a-c)}$++$\frac{b}{(b-a)(b-c)}$+$\frac{c}{(c-a)(c-b)}$]+x[$\frac{a}{(a-b)(a-c)}$++$\frac{b}{(b-a)(b-c)}$+$\frac{c}{(c-a)(c-b)}$]
=0+x×0
=0+0
=0;
(2)$\frac{{a}^{3}}{(a-b)(a-c)}$+$\frac{{b}^{3}}{(b-c)(b-a)}$+$\frac{{c}^{3}}{(c-a)(c-b)}$
=$\frac{{a}^{3}}{(a-b)(a-c)}$-$\frac{{b}^{3}}{(a-b)(b-c)}$+$\frac{{c}^{3}}{(a-c)(b-c)}$
=$\frac{{a}^{3}(b-c)-{b}^{3}(a-c)+{c}^{3}(a-b)}{(a-b)(a-c)(b-c)}$,
a3(b-c)-b3(a-c)+c3(a-b)
=a3(b-c)-b3(a-b+b-c)+c3(a-b)
=a3(b-c)-b3(a-b)-b3(b-c)+c3(a-b)
=(b-c)(a3-b3)-(a-b)(b3-c3)
=(b-c)(a-b)(a2+ab+b2)-(b-c)(a-b)(b2+bc+c2)
=(b-c)(a-b)(a2+ab+b2-b2-bc-c2)
=(b-c)(a-b)(a2-c2+ab-bc)
=(b-c)(a-b)[(a+c)(a-c)+b(a-c)]
=(b-c)(a-b)(a-c)(a+b+c),
则$\frac{{a}^{3}}{(a-b)(a-c)}$+$\frac{{b}^{3}}{(b-c)(b-a)}$+$\frac{{c}^{3}}{(c-a)(c-b)}$
=$\frac{(a-b)(a-c)(b-c)(a+b+c)}{(a-b)(a-c)(b-c)}$
=a+b+c.
点评 考查了分式的加减法,本题难度较大,关键是拆项法,因式分解法的灵活运用.


科目:初中数学 来源: 题型:选择题
| 工种 | 人数 | 每人每月工资/元 |
| 电工 | 6 | 7000 |
| 木工 | 4 | 6000 |
| 瓦工 | 6 | 5000 |
| A. | 变大 | B. | 不变 | C. | 变小 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
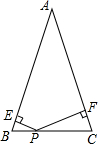 如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )
如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )| A. | 2.5cm | B. | 2$\sqrt{2}$cm | C. | 5cm | D. | 2$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
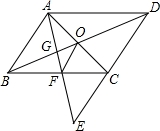 如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.
如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com