
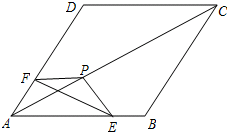
 如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6$\sqrt{3}$,∠BAD=60°,且AB>6$\sqrt{3}$.
如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6$\sqrt{3}$,∠BAD=60°,且AB>6$\sqrt{3}$.分析 (1)作PG⊥AB于G,PH⊥AD于H,由菱形的性质得出AC平分∠BAD,由角平分线的性质得出PG=PH,由HL证明Rt△PGE≌Rt△PHF,得出∠HPF=∠GPE,GE=HF,求出∠GPH=120°,即可得出∠EPF=120°;
(2)由菱形的性质得出∠PAG=30°,由含30°角的直角三角形的性质得出PG=$\frac{1}{2}$AP=4,由勾股定理求出AG=$\sqrt{3}$PG=4$\sqrt{3}$,求出AE+AF=2AG=8$\sqrt{3}$即可.
解答 解:(1)作PG⊥AB于G,PH⊥AD于H,如图所示: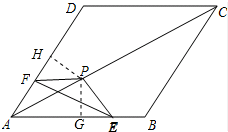
则∠PGE=∠PHF=90°,
∵四边形ABCD是菱形,
∴AC平分∠BAD,
∴PG=PH,
在Rt△PGE和Rt△PHF中,$\left\{\begin{array}{l}{EP=FP}\\{PG=PH}\end{array}\right.$,
∴Rt△PGE≌Rt△PHF(HL),
∴∠HPF=∠GPE,GE=HF,
∵∠BAD=60°,
∴∠GPH=120°,
∴∠EPF=120°;
(2)∵∠BAD=60°,AC平分∠BAD,
∴∠PAG=30°,
∴PG=$\frac{1}{2}$AP=4,
∴AG=$\sqrt{3}$PG=4$\sqrt{3}$,
∴AE+AF=AG+GE+AH-HF=2AG=8$\sqrt{3}$.
点评 本题考查了菱形的性质、角平分线的性质、全等三角形的判定与性质、含30°角的直角三角形的性质、勾股定理等知识;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小红去商场买了2个单价为a元的本子和3支单价为b元的笔,她共花了多少钱? | |
| B. | 全班同学都报名参加了课外活动小组,其中报2个小组的有a名同学,报3个小组的有b名同学,全班共有多少名同学? | |
| C. | 小亮看书特别快,他借了一本课外书,5天就看完了,他有两天是每天看a页,有三天是每天看b页,这本书一共有多少页? | |
| D. | 为了奖励“学雷锋先进个人”,学校买了两种奖品,其中2元的笔记本a本,3元的笔记本b本,学校买这些奖品共花了多少钱? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com