练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．（1）解不等式3（x-1）＜5x+2，并在数轴上表示解集．
    （2）解方程：$\frac{5x-4}{2x-4}$=$\frac{2x+5}{3x-6}$-$\frac{1}{2}$．

    分析 （1）不等式去括号，移项合并，把x系数化为1，求出解集，表示在数轴上即可；
    （2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

    解答 解：（1）去括号得：3x-3＜5x+2，
    移项合并得：2x＞-5，
    解得：x＞-2.5，
    ；
    （2）去分母得：15x-12=4x+10-3x+6，
    移项合并得：14x=28，
    解得：x=2，
    经检验x=2是增根，分式方程无解．

    点评 此题考查了解分式方程，以及解一元一次不等式，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    17．当x＜5时，$\sqrt{（x-5）^{2}}$的值是5-x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．分式方程$\frac{2}{x-1}=\frac{x+4}{1-{x}^{2}}$的解是x=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．在一个不透明的袋子中装有仅颜色不同的3个白球和1个红球，先从袋子中随机摸出一个球记下颜色放回，再随机地摸出一个球，则两次都摸到白球的概率为$\frac{9}{16}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在索契冬奥会中，中国体育代表团取得了3金、4银、2铜的好成绩，某校为了解同学对短道速滑、滑雪、花样滑冰三个项目的喜爱情况，随机抽取了一定数量的同学进行调查，得到如下统计图表．
    喜爱的运动项目统计
    项目短道速滑滑雪花样滑冰
    频数25a10
    频率50%30%b
    请你根据统计图、表提供的信息解答下列问题：
    （1）这次随机抽取了50名学生进行调查；
    （2）统计表中a、b的值分别为：a=15，b=20%；
    （3）在统计图中“滑雪”部分扇形所对应的圆心角是108度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算：
    （1）$\sqrt{27}$-3tan30°-（$\frac{1}{2}$）-2-4（$\sqrt{3}$-2）2
    （2）6tan230°-$\sqrt{3}$sin60°-cos45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．移动互联网已全面进入人们的日常生活，某市4G用户总数达到3820000，数据3820000用科学记数法表示为（　　）
    A．3.8×106B．3.82×105C．3.82×106D．3.82×107

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．广东省“二孩”政策已经正式开始实施，给我们的生活可能带来一些变化，广州市某区计生部门抽样调查了部分市民对变化的看法（每个参与调查的市民必须在以下6种变化中选出自己认为最明显的一项变化），并将调查结果绘制成统计图：
     种类 A选项 B选项 C选项 D选项 E选项 F选项
     实施“二孩”的可能变化 延缓社会老龄化 家庭发展能力提升 导致人口暴增 增加公共资源压力 出生人口性别趋衡 劳动年龄人口增加

    根据统计图，回答下列问题：
    （1）参与调查的市民一共有2000人；
    （2）请补全条形统计图；
    （3）求∠α；
    （4）若该区有155万常住人口，对于二孩政策的实施给生活带来的变化，请估计该区有多少万人会选择B选项“家庭发展能力提升”？

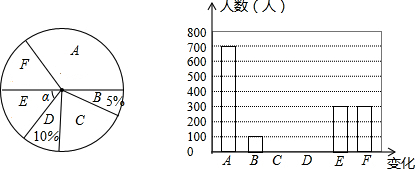
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

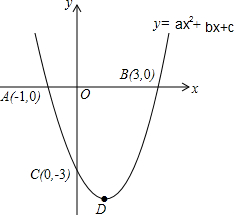    17．如图，抛物线y=ax2+bx+c的图象与x轴交于A（-1.0），B（3，0）两点，与y轴交于点C（0，-3），顶点为D．
    （1）求此抛物线的解析式．
    （2）求此抛物线顶点D的坐标和对称轴．
    （3）探究对称轴上是否存在一点P，使得以点P、D、A为顶点的三角形是等腰三角形？若存在，请求出所有符合条件的P点的坐标，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案