
分析 首先根据每个加数的特征,把每个加数拆分成两个数的和的形式,然后再把拆分后的每个数分成两个分数的差的性质,再应用加法交换律和加法结合律,求出算式$\frac{5}{1×2×3}+\frac{7}{2×3×4}$+…+$\frac{19}{8×9×10}$的值是多少即可.
解答 解:$\frac{5}{1×2×3}+\frac{7}{2×3×4}$+…+$\frac{19}{8×9×10}$
=$\frac{1}{1×2}+\frac{1}{1×3}$$+\frac{1}{2×3}+\frac{1}{2×4}$$+…+\frac{1}{8×9}+\frac{1}{8×10}$
=($\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{8×9}$)+($\frac{1}{1×3}+\frac{1}{2×4}+\frac{1}{3×5}+…+\frac{1}{8×10}$)
=($1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{8}-\frac{1}{9}$)+$\frac{1}{2}×$(1-$\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{8}-\frac{1}{10}$)
=(1-$\frac{1}{9}$)+$\frac{1}{2}×$(1$+\frac{1}{2}-\frac{1}{9}-\frac{1}{10}$)
=$\frac{8}{9}+\frac{29}{45}$
=$\frac{23}{15}$
故答案为:$\frac{23}{15}$.
点评 (1)此题主要考查了有理数的混合运算,要熟练掌握,解答此题的关键是要明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,并能把每个加数拆分.
(2)此题还考查了加法运算定律的应用,要熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
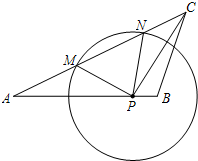 如图,已知在△ABC中,AB=15,AC=20,tanA=$\frac{1}{2}$,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.
如图,已知在△ABC中,AB=15,AC=20,tanA=$\frac{1}{2}$,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
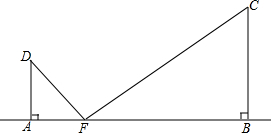 一条宽阔的街道的两侧有两个建筑物AD和BC,王洋在街道的两建筑物之间测AD的仰角为45°,建筑物BC的仰角为57°,已知两建筑物的高度之和为60米,两街道宽AB=50米,求建筑物BC的高度.(sin57°≈0.83,cos57°≈0.54,tan57≈1.5)
一条宽阔的街道的两侧有两个建筑物AD和BC,王洋在街道的两建筑物之间测AD的仰角为45°,建筑物BC的仰角为57°,已知两建筑物的高度之和为60米,两街道宽AB=50米,求建筑物BC的高度.(sin57°≈0.83,cos57°≈0.54,tan57≈1.5)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,求他一次就能猜中的概率.
在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,求他一次就能猜中的概率.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com