
分析 根据题意可以画出相应的图形,从而可以解答本题.
解答 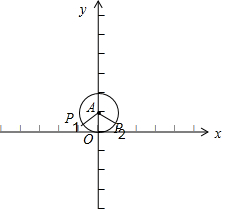 解:如图所示,
解:如图所示,
当点P在点P1的位置时,点P第n次落在x轴上时,点P的横坐标为:x=$\frac{(360-120)π×1}{180}+(n-1)×2π×1$=$\frac{6nπ-2π}{3}$,即此时点P的坐标为($\frac{6nπ-2π}{3}$,0);
当点P在点P2的位置时,点P第n次落在x轴上时,点P的横坐标为:x=$\frac{60×π×1}{180}+(n-1)×2π×1$=$\frac{6nπ-5π}{3}$,即此时点P的坐标为($\frac{6nπ-5π}{3}$,0);
故答案为:($\frac{6nπ-2π}{3}$,0)或($\frac{6nπ-5π}{3}$,0).
点评 本题考查切线的性质、点的坐标,解题的关键是明确题意,画出相应的图形,利用数形结合的思想解答.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:填空题
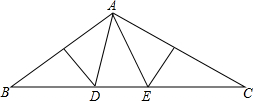 如图,△ABC的两边AB、AC的垂直平分线分别交边BC于点D、E,若△ABC的周长为26,AB+AC=14,则△ABE和△ACD的周长和是38.
如图,△ABC的两边AB、AC的垂直平分线分别交边BC于点D、E,若△ABC的周长为26,AB+AC=14,则△ABE和△ACD的周长和是38.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
| 身高 | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com