练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．在直角三角形ABC中，∠C=90°，BC=12，CA=5，AB=13．

    分析 直接根据勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方进行计算即可．

    解答 解：根据勾股定理可得AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13，
    故答案为：13．

    点评 此题主要考查了勾股定理，关键是掌握如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．（1）解方程：$\frac{3x+1}{2}$-2=$\frac{3x-2}{10}$
    （2）在等式y=kx+b中，当x=1时，y=2；x=2时，y=1；当x=3时，y=a，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图是根据某市2010年至2014年的工业生产总值绘制的条形统计图，观察统计图可以看出，工业生产总值（亿元）增长最多的年份是2014年．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．如图，下列条件中能判断BD∥AC的是（　　）
    A．∠1=∠2B．∠D=∠AC．∠3=∠4D．∠ABD+∠D=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．在同一平面直角坐标系中，观察以下直线：y=2x，y=-x+6，y=x+2，y=4x-4图象的共同特点，若y=kx+5也有该特点，试求满足条件的k值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

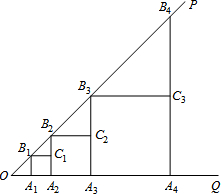    13．如图所示，∠POQ=45°，点A1是射线OQ上一点，且OA1=1，过点A1作A1B1⊥OQ，与OP交于点B1，以A1B1为边作第一个正方形A2A1B1C1；延长A2C1与OP交于点B2，再以A2B2为边作第二个正方形A3A2B2C2；延长A3C2与OP交于点B3，再以A3B3为边作第三个正方形A4A3B3C3；延长A4C3…则第2个正方形的边长为4；第三个正方形A4A3B3C3的面积是16；第n（n是正整数）个正方形的面积（用含n的式子表示）是22n-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列图形中，既是中心对称图形又是轴对称图形的是（　　）
    A．等边三角形B．矩形C．等腰梯形D．平行四边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

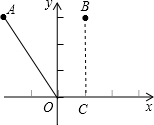    17．对于两个已知图形G1、G2，在G1上任取一点P，在G2上任取一点Q，当线段PQ的长度最小时，我们称这个最小长度为G1、G2的“密距”．例如，如上图，A（-2，3），B（1，3），C（1，0），则点A与射线OC之间的“密距”为$\sqrt{13}$，点B与射线OC之间的“密距”为3．如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$，则k值为（　　）
    A．k=4B．k=-4C．k=6D．k=-6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．化简：m+2+$\frac{4}{m-2}$．

    查看答案和解析>>

    同步练习册答案