
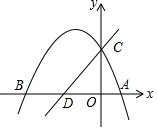
 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+bx+c的顶点为(-3,$\frac{25}{4}$),与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C,D是BO的中点,直线DC的解析式为y=kx+4.
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+bx+c的顶点为(-3,$\frac{25}{4}$),与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C,D是BO的中点,直线DC的解析式为y=kx+4.分析 (1)设抛物线的解析式为y=a(x+3)2+$\frac{25}{4}$,把点C(0,4)代入求出a即可解决问题.
(2)先求出A、B、D坐标,再根据三角形面积公式计算即可.
(3)S△BDP=S△BDC,推出点P的纵坐标为4或-4,列出方程解方程即可解决问题.
(4)①如图2中,连接OP,设P[m,-$\frac{1}{4}$(m+3)2+$\frac{25}{4}$],根据S△PCD=S△POD+S△POC-S△OCD计算即可.
②利用配方法即可解决问题.
③根据题意列出方程即可解决问题.
解答 解:(1)设抛物线的解析式为y=a(x+3)2+$\frac{25}{4}$,
由题意抛物线经过点C(0,4),
∴4=9a+$\frac{25}{4}$,
∴a=-$\frac{1}{4}$,
∴抛物线的解析式为y=-$\frac{1}{4}$(x+3)2+$\frac{25}{4}$.
(2)对于抛物线y=-$\frac{1}{4}$(x+3)2+$\frac{25}{4}$,令y=0,得到-$\frac{1}{4}$(x+3)2+$\frac{25}{4}$=0,解得x=-8或2,
∴B(-8,0),A(2,0),
∵D是OB中点,
∴D(-4,0),
∴S△ADC=$\frac{1}{2}$•AD•OC=$\frac{1}{2}$×6×4=12.
(3)如图1中,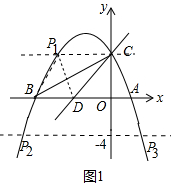
∵S△BDP=S△BDC,
∴点P的纵坐标为4或-4,
当y=4时,-$\frac{1}{4}$(x+3)2+$\frac{25}{4}$=4,解得x=-6或0,
y=-4时,-$\frac{1}{4}$(x+3)2+$\frac{25}{4}$=-4,解得x=-3±$\sqrt{41}$,
∴P1(-6,4),P2(-3-$\sqrt{41}$,-4),P3(-3+$\sqrt{41}$,-4).
(4)①如图2中,连接OP,设P(t,-$\frac{1}{4}$(t+3)2+$\frac{25}{4}$).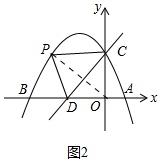
∴S△PCD=S△POD+S△POC-S△OCD=$\frac{1}{2}$×4×[-$\frac{1}{4}$(t+3)2+$\frac{25}{4}$]+$\frac{1}{2}$×4×(-t)-$\frac{1}{2}$×4×4=-$\frac{1}{2}$t2-5t.
②∵S=-$\frac{1}{2}$t2-5t=-$\frac{1}{2}$(t+5)2+$\frac{25}{2}$,
∵-$\frac{1}{2}$<0,
∴t=-5时,S有最大值=$\frac{25}{2}$,此时P(-5,$\frac{21}{4}$).
③由题意可知:$\frac{1}{2}$×4×(-$\frac{1}{4}$t2-$\frac{3}{2}$t+4):(-$\frac{1}{2}$t2-5t)=2:3或$\frac{1}{2}$×4×(-$\frac{1}{4}$t2-$\frac{3}{2}$t+4):(-$\frac{1}{2}$t2-5t)=3:2,
解得:t=8或-6或-2或-16,
t=8和-16不合题意舍弃,
∴t的值为-2或-6.
点评 本题考查二次函数综合题、待定系数法、三角形的面积等知识,解题的关键是学会用方程的思想思考问题,把问题转化为方程解决,属于中考压轴题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:填空题
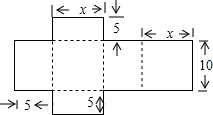 如图,已知某长方体的展开图的面积为310cm2,根据图中数据可列出关于x的一元一次方程为2×(10x+5x+5×10)=310,x的值为7.
如图,已知某长方体的展开图的面积为310cm2,根据图中数据可列出关于x的一元一次方程为2×(10x+5x+5×10)=310,x的值为7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
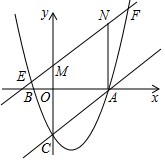 已知抛物线y=x2-2x-3,与x轴交于A、B两点,与y轴交于C点,EF∥AC交y轴于M,AN∥y轴交EF于N点,求$\frac{EM}{FN}$的值.
已知抛物线y=x2-2x-3,与x轴交于A、B两点,与y轴交于C点,EF∥AC交y轴于M,AN∥y轴交EF于N点,求$\frac{EM}{FN}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50cm,EF=25cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB=( )m.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50cm,EF=25cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB=( )m.| A. | 4 m | B. | 5m | C. | 6.6m | D. | 7.7m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com