
【题目】甲、乙两个仓库共存有粮食60![]() .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:
(1)甲仓库运进粮食14![]() ,乙仓库运出粮食10
,乙仓库运出粮食10![]() 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
(2)如果甲仓库原有的粮食比乙仓库的2倍少3![]() ,则甲仓库运出多少
,则甲仓库运出多少![]() 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
(3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1![]() ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8![]() 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少![]() ?
?
【答案】(1)原来甲仓库有18t粮食,乙仓库有42t粮食;(2)甲仓库运出9t粮食给乙仓库,可使甲、乙两仓库粮食数量相等(3)甲乙两仓库共存有粮食95t
【解析】试题分析:(1)设甲有xt,则乙有(60-x)t,根据甲仓库运进粮食14t,乙仓库运出粮食10t后,两个仓库的粮食数量相等,可得出方程,解出即可;
(2)先求出甲乙粮仓原有多少粮食,再求甲运出的粮食数量即可;
(3)根据题意列出代数式求值 即可.
试题解析:(1)设甲仓库原有粮食xt,则乙仓库原有粮食(60-x)t,
由题知x+14=(60-x)-10,解得x=18.
当x=18时,60-x=42.
∴原来甲仓库有18t粮食,乙仓库有42t粮食;
(2)设甲仓库原有粮食xt,则乙仓库原有粮食(60-x)t,
由题知x=2(60-x)-3,解得x=39.
当x=39时,60-x=21.
∴原来甲仓库有39t粮食,乙仓库有21t粮食.
设甲仓库运出yt粮食给乙仓库,可使甲、乙两仓库粮食数量相等,
由题知39-y=21+y,解得y=9,
∴甲仓库运出9t粮食给乙仓库,可使甲、乙两仓库粮食数量相等.
(3)设甲仓库原有粮食xt,乙仓库原有粮食yt,则x+y=60.
设运进粮食后,两仓库共有粮食wt,则
w=60+(![]() x+1)+
x+1)+![]() (y+8)=65+
(y+8)=65+![]() (x+y)=65+30=95,
(x+y)=65+30=95,
∴此时甲乙两仓库共存有粮食95t.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
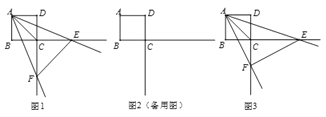
【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF。设CE=a,CF=b。
(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同.小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=-x+5的图象上的概率;
(3)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜,若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由;若不公平,请写出公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一幅三角板按照如图所示的位置放置在直线![]() 上,
上, ![]() =
=![]() =45°,
=45°,![]() =
=![]() =90°,
=90°,![]() =30°,
=30°,![]() =60°.将含45°锐角的三角板
=60°.将含45°锐角的三角板![]() 固定不动,含30°锐角的三角板
固定不动,含30°锐角的三角板![]() 绕点
绕点![]() 顺时针旋转1周,在此过程中:
顺时针旋转1周,在此过程中:
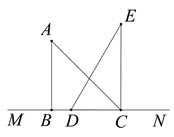
(1)如图,当点![]() 在
在![]() 内部时,连接
内部时,连接![]() .
.
①若![]() 平分
平分![]() ,试问
,试问![]() 是否也平分
是否也平分![]() ?请说明理由.
?请说明理由.
②若![]() ,
, ![]() ,
, ![]() ,试探究
,试探究![]() 、
、![]() 、
、![]() 这三者之间有什么数量关系?请用一个含
这三者之间有什么数量关系?请用一个含![]() 、
、![]() 、
、![]() 的等式来表达,并说明理由.
的等式来表达,并说明理由.
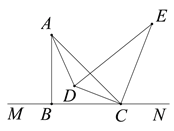
(2)如图, ![]() 是
是![]() 的角平分线,当
的角平分线,当![]() 所在直线与
所在直线与![]() 所在直线互相垂直时,请直接写出
所在直线互相垂直时,请直接写出![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
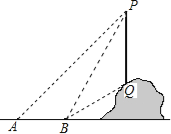
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com