
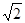 ,
,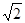 )、(1,1)、(2+
)、(1,1)、(2+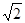 ,
,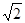 )
)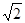 ,2
,2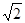 ),(4+2
),(4+2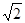 ,-2
,-2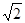 );
);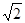 ,2
,2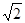 ),(4+2
),(4+2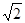 ,-2
,-2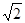 )。
)。

科目:初中数学 来源:不详 题型:单选题
 轴上的垂足分别为A1、B1,若OA1+OB1>4,则△OA1A的面积S1与△OB1B的面积S2的大小关系是( ).
轴上的垂足分别为A1、B1,若OA1+OB1>4,则△OA1A的面积S1与△OB1B的面积S2的大小关系是( ). 
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 销售方式 | 批发 | 零售 | 冷库储藏后销售 |
| 售价(元/吨) | 3000 | 4500 | 5500 |
| 成本(元/吨) | 700 | 1000 | 1200 |
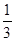 求y与x之间的函数关系;
求y与x之间的函数关系;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
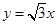 ,点
,点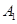 坐标为(1,0),过点
坐标为(1,0),过点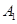 作
作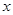 轴的垂线交直线于点
轴的垂线交直线于点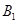 ,以原点
,以原点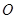 为圆心,
为圆心,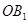 长为半径画弧交
长为半径画弧交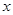 轴于点
轴于点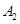 ;再过点
;再过点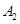 作
作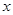 轴的垂线交直线于点
轴的垂线交直线于点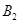 ,以原点
,以原点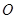 为圆心,
为圆心,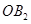 长为半径画弧交
长为半径画弧交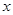 轴于点
轴于点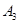 ,…,按此做法进行下去,点A1011的坐标为
,…,按此做法进行下去,点A1011的坐标为 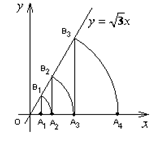
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ),直线l2的函数表达式为
),直线l2的函数表达式为 ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M. 时a的值.
时a的值. 半径R=
半径R= ,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com