
 如图所示,六盘水高铁站在南宁市45°扇形辐射区域内,要求到“昆明”和“贵阳”的距离相等,又同时保证高铁站到“云广连线”和“贵广连线”距离相同.
如图所示,六盘水高铁站在南宁市45°扇形辐射区域内,要求到“昆明”和“贵阳”的距离相等,又同时保证高铁站到“云广连线”和“贵广连线”距离相同.分析 “昆明”和“贵阳”是线段BC的两个端点,到“昆明”和“贵阳”的距离相等,意味着到线段BC的两个端点的距离相等,故需作线段BC的垂直平分线;到“云广连线”和“贵广连线”距离相同,意味着到∠BAC的两边距离相等,故需作∠BAC的角平分线,要同时满足这两个要求,就取它们的交点.
解答 解:(1)盘县
(2)如图:作∠BAC的角平分线,再作线段BC垂直平分线,它们的交点便就是“冯家庄”的位置. 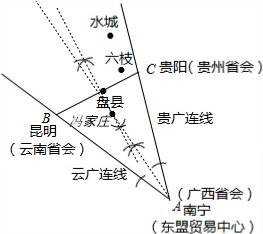
(3)答:线段的垂直平分线上的点到线段的两个端点的距离相等,而且角的平分线上的点到角的两边的距离相等,所以所作线段的垂直平分线与角平分线的交点保证了 六盘水高铁站在南宁市45°扇形辐射区域内,到“昆明”和“贵阳”的距离相等,又同时保证高铁站到“云广连线”和“贵广连线”距离相同.
点评 本题考查了应用与设计作图,解题的关键是掌握线段的垂直平分线的作法及意义、角平分线的作法及意义.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,△ABC中,CD是∠ACB的角平分线.
已知,如图,△ABC中,CD是∠ACB的角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com