
【题目】如图,△ABC为等腰直角三角形,△ABD为等边三角形,连接CD

(1)求∠ACD的度数
(2)作∠BAC的角平分线交CD于点E,求证:DE=AE+CE
(3)在(2)的条件下,P为图形外一点,满足∠CPB=60°,求证:EP平分∠CPB.
【答案】(1)15°;(2)见解析;(3)见解析
【解析】
(1)由等腰直角三角形和等边三角形的性质可得![]() ,
,![]() ,从而可得
,从而可得![]() ,再根据等腰三角形的性质和三角形内角和定理即可得;
,再根据等腰三角形的性质和三角形内角和定理即可得;
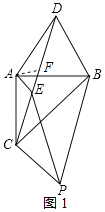
(2)如图1(见解析),在ED上截取![]() ,连接AF,可证
,连接AF,可证![]() 是等边三角形,得出
是等边三角形,得出![]() ,再证明
,再证明![]() ,由三角形全等的性质可得
,由三角形全等的性质可得![]() ,即可得证;
,即可得证;
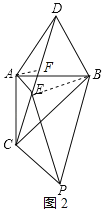
(3)如图2(见解析),连接BE,证明![]() ,得出
,得出![]() ,
,![]() ,从而可求出
,从而可求出![]() ,得出
,得出![]() ,证出B、E、C、P四点共圆,由圆周角定理得出
,证出B、E、C、P四点共圆,由圆周角定理得出![]() ,即可得证.
,即可得证.
(1)![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为等边三角形
为等边三角形
![]()
![]()
![]() ;
;
(2)如图1,在ED上截取![]() ,连接AF
,连接AF
![]() ,AE平分
,AE平分![]()
![]()
![]()
![]() 是等边三角形,
是等边三角形,
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,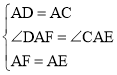
![]()
![]()
![]() ;
;
(3)如图2,连接BE
在![]() 和
和![]() 中,
中,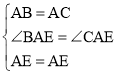
![]()
![]()
![]()
![]()
![]()
∴B、E、C、P四点共圆
![]() (圆周角定理)
(圆周角定理)
![]() 平分
平分![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,BO、CO 分别平分∠ABC、∠ACB,DE 经过点 O, 且 DE∥BC,DE 分别交 AB、AC 于 D、E,则图中等腰三角形的个数为( )

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法①△BDF≌△CDE;②△ABD和△ACD面积相等;③BF∥CE;④CE=BF.其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
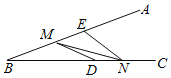
【题目】如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并完成下列问题
通过观察,发现方程:x+![]() =2+
=2+![]() 的解是:x1=2,x2=
的解是:x1=2,x2=![]() ;
;
x+![]() =3+
=3+![]() 的解是:x1=3,x2=
的解是:x1=3,x2=![]() ;
;
x+![]() =4+
=4+![]() 的解是:x1=4,x2=
的解是:x1=4,x2=![]() ;
;
……
(1)观察方程的解,猜想关于x的方程x+![]() =10+
=10+![]() 的解是 ;根据以上规律,猜想关于x的方程x+
的解是 ;根据以上规律,猜想关于x的方程x+![]() =m+
=m+![]() 的解是 ;
的解是 ;
(2)利用上述规律解关于x的方程![]() =a+
=a+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,灯杆AB与墙MN的距离为18米,小丽在离灯杆(底部)9米的D处测得其影长DE为3m,设小丽身高为1.6m.
(1)求灯杆AB的高度;
(2)小丽再向墙走7米,她的影子能否完全落在地面上?若能,求此时的影长;若不能,求落在墙上的影长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知正方形ABCD,E是AD上一点,F是BC上一点,G是AB上一点,H是CD上一点,线段EF、GH交于点O,∠EOH=∠C,求证:EF=GH;
(2)如图2,若将“正方形ABCD”改为“菱形ABCD”,其他条件不变,探索线段EF与线段GH的关系并加以证明;
(3)如图3,若将“正方形ABCD”改为“矩形ABCD”,且AD=mAB,其他条件不变,探索线段EF与线段GH的关系并加以证明;

附加题:根据前面的探究,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题,画出图形,并证明,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成相应任务:



(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是 命题(填“真”或“假”).
(2)小彬经过探究发现命题②是真命题.请你结合图2证明这一命题.
(3)小颖经过探究又提出了一个新的命题:“若![]() ,
,![]() ,
,![]() , , ,则四边形
, , ,则四边形![]() ≌四边形
≌四边形![]() ”请在横线上填写两个关于“角”的条件,使该命题为真命题.
”请在横线上填写两个关于“角”的条件,使该命题为真命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,A、B、C、D、E五位老师作为评委,对演讲答辩得分进行评价,结果如演讲答辩得分表,另全班50位同学则参与民主测评进行投票,结集如图.
A | B | C | D | E | |
甲 | 90 | 92 | 94 | 95 | 88 |
乙 | 89 | 86 | 87 | 94 | 91 |

规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好“票数×1分+“一般”票数×0分.
(1)求甲、乙两位选手各自演讲答辩的得分
(2)求甲、乙两位选手各自民主测评的得分
(3)若演讲答辩得分和民主测评得分按2∶3的权重比计算两位选手的综合得分,则应选取哪位选手当班长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com