
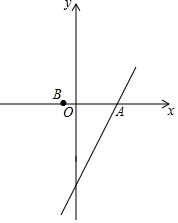 已知抛物线y1=a(x-x1)(x-x2)(a≠0,x1≠x2)与x轴分别交于A(x1,0)、
已知抛物线y1=a(x-x1)(x-x2)(a≠0,x1≠x2)与x轴分别交于A(x1,0)、分析 (1)①根据已知条件得到当a=1,得到y1=(x-3)(x+1),由于直线y2=2x+t经过点A,得到方程0=2×3+t,得到t=-6,于是得到结论;
②设y1=a(x-3)(x+1),根据题意得不等式,即可得到结论;
(2)根据已知条件得到y=y1+y2=a(x-x1)(x-x2)+2x-2x1=(x-x1)[a(x-x1)+2]根据函数y的图象与x轴仅有一个公共点,于是得到结论.
解答 解:(1)①∵已知抛物线y1=a(x-x1)(x-x2)经过A(x1,0)、B(x2,0)两点,当a=1,
∴y1=(x-3)(x+1),
∵直线y2=2x+t经过点A,
∴0=2×3+t,
解得:t=-6,
∴y2=2x-6;
②设y1=a(x-3)(x+1),
由题意可得,当x=4时,y1=5a<2,
∴a<$\frac{2}{5}$,
当x=5时,y1=12a>4,
∴a>$\frac{1}{3}$,
∴$\frac{1}{3}<$a<$\frac{2}{5}$;
(2)∵直线y2过点A(x1,0),
∴0=2x1+t,∴t=-2x1,
∴y=y1+y2=a(x-x1)(x-x2)+2x-2x1=(x-x1)[a(x-x1)+2]
∴方程的根为x1,x2-$\frac{2}{a}$,
∵函数y的图象与x轴仅有一个公共点,
∴x1=x2-$\frac{2}{a}$,
∴x2-x1=$\frac{2}{a}$.
点评 本题考查了抛物线与x轴的交点,一次函数图象上点的坐标特征,二次函数图象上点的坐标特征,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
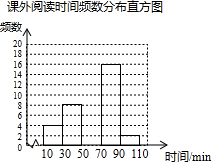 某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如图不完整的统计图表.
某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如图不完整的统计图表.| 课外阅读时间t | 频数 | 百分比 |
| 10≤t<30 | 4 | 8% |
| 30≤t<50 | 8 | 16% |
| 50≤t<70 | a | 40% |
| 70≤t<90 | 16 | b |
| 90≤t<110 | 2 | 4% |
| 合计 | 50 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
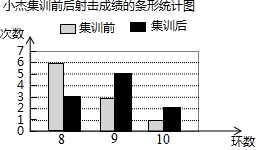 为了解射击运动员小杰的集训效果,教练统计了他集训前后的两次测试成绩(每次测试射击10次),制作了如图所示的条形统计图.
为了解射击运动员小杰的集训效果,教练统计了他集训前后的两次测试成绩(每次测试射击10次),制作了如图所示的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一个粒子在第一象限内及x、y轴上运动,在第一分钟内它从原点O运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向上来回运动,且每分钟移动1个长度单位,那么2017分钟后这个粒子所处的位置是( )
如图,一个粒子在第一象限内及x、y轴上运动,在第一分钟内它从原点O运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向上来回运动,且每分钟移动1个长度单位,那么2017分钟后这个粒子所处的位置是( )| A. | (7,45) | B. | (8,44) | C. | (44,7) | D. | (45,8) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
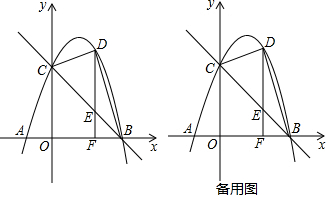
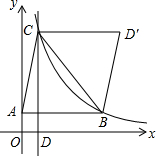 如图,在△ABC中,B、C两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,且BC=$\frac{3k}{4}$,S△ABC=$\frac{3k}{2}$,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为8.
如图,在△ABC中,B、C两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,且BC=$\frac{3k}{4}$,S△ABC=$\frac{3k}{2}$,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>1 | B. | m>0 | C. | m<1 | D. | m<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
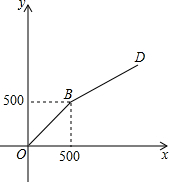 “六一”儿童节期间,甲、乙两家网店以同样价格销售相同的儿童用品,他们的优惠方案分别为:甲店,一次性购物超过100元后的价格部分打七折;乙店,一次性购物超过500元后的价格部分打五折.设商品原价为x元,购物应付金额为y元.
“六一”儿童节期间,甲、乙两家网店以同样价格销售相同的儿童用品,他们的优惠方案分别为:甲店,一次性购物超过100元后的价格部分打七折;乙店,一次性购物超过500元后的价格部分打五折.设商品原价为x元,购物应付金额为y元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com