
【题目】(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
②如果欲求![]() 的值,可令
的值,可令
![]() ……………①
……………①
将①式右边顺序倒置,得![]() ……………②
……………②
由②加上①式,得2![]() ;
;
∴ S=_________________;
由结论求![]() ;
;
(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
②为了求![]() 的值,可令
的值,可令![]() ,则
,则![]() ,因此
,因此![]() ,所以
,所以![]() ,
,
即![]() .
.
仿照以上推理,计算![]()
【答案】(1)①1,18,n;②![]() ,
,![]() ,1540;(2)①2,
,1540;(2)①2,![]() ,
,![]() ;②
;②![]() .
.
【解析】
(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差都为1,从而可得常数为1;根据此规律,如果![]() 为正整数)=n,据此即可求得答案;
为正整数)=n,据此即可求得答案;
②观察可得2![]() n(n+1),从而求得 S;根据上面得到的式子进行计算即可求得
n(n+1),从而求得 S;根据上面得到的式子进行计算即可求得![]() 的值;
的值;
(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数2,根据此规律,可得![]() 为正整数)=2n,据此即可得答案;
为正整数)=2n,据此即可得答案;
②根据推理进行计算即可求得![]() 的值.
的值.
(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是1;根据此规律,如果![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() 18,
18,![]() n,
n,
故答案为:1,18,n;
②令![]() ,①
,①
将①式右边顺序倒置,得![]() ,②
,②
②+①,得2![]()
![]() =n(1+n),
=n(1+n),
∴ S=![]() ;
;
![]() =
=![]() =1540,
=1540,
故答案为:![]() ,
,![]() ,1540;
,1540;
(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是2;根据此规律,如果![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() 218,
218,![]() 2n,
2n,
故答案为:2,![]() ,
,![]() ;
;
②令![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )
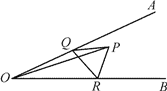
A. 6 B. 12 C. 16 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:数轴上有A、B两点,分别对应的数为a,b,已知(a+1)2与|b﹣3|互为相反数.点P为数轴上一动点,对应为x.
(1)a= ;b=
(2)若点P到点A和点B的距离相等,则点P对应的数是
(3)数轴上是否存在点P,使点P到点A和点B的距离之和为5?若存在,请求出x的值;若不存在,说明理由;
(4)|x﹣a|+|x﹣b|的最小值=
(5)当点P以每分钟1个单位长度的速度从O点向左运动,点A以每分钟5个单位长度向左运动,问几分钟时点P到点A、点B的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样大小的围棋子按如图所示的方式摆图案,按照这样的规律摆下去,第12个图案的围棋子个数是( )

A. 16 B. 28 C. 29 D. 38
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(![]() ,-1)中,是“垂点”的点为 ;
,-1)中,是“垂点”的点为 ;
(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是![]() ,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为8.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
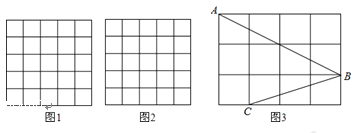
(1)在图1中以格点为顶点画一个面积为5的等腰直角三角形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、 ![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,反比例函数和二次函数y=k(x2+x﹣1)的图象交于点A(1,k)和点B(﹣1,﹣k).
(1)当k=﹣2时,求反比例函数的解析式;
(2)要使反比例函数和二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围;
(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
(4)点C为x轴上一动点,且C点坐标为(2k,0),当△ABC是以AB为斜边的直角三角形时,求K的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com